A statue 4 meters high sits on a column 5.6 meters high . How far from the column must a man, whose eye level is 1.6 meters from the ground, stand in order to see the statue at the greatest angle ?
Step by step video & image solution for A statue 4 meters high sits on a column 5.6 meters high . How far from the column must a man, whose eye level is 1.6 meters from the ground, stand in order to see the statue at the greatest angle ? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A statue 4 metres high sits on a column 5.6 metres high. How far from the column must a man,whose eye level is 1.6 metres from the ground, stand in order to have the most favourable view of the statue.
View SolutionA statue 8 meters high standing on the top of a tower 64 meters high, on the bank of a river, subtends at a point A on the opposite bank, directly facing the tower, the same angle as subtends at the same point A by man of height 2 meters standing at the base of the tower. Prove that the breadth of the river is 16√6 meters.
View Solution
Knowledge Check
A candle flame 2 cm high is placed at distance of 2 meter from a wall. How far from the wall must a concave mirror to placed in order to form an image of the flame 6 cm high on the wall ?
A225 cmB300cmC450 cmD500 cmA man is moving away from a tower 41.6m high at a rate of 2ms−1. If the eye level of the man is 1.6m above the ground, then the rate at which the angle of elevation of the top of the tower changes, when he is at a distance of 30 m from the foot of the tower, is:
A−4125 radian/sB225 radian/sC−1625 radian/sDNone of theseA pole 25 meters long stands on the top of a tower 225 meters high. It θ is the angle subtended by the pole at a point on the ground which is at distance 2.25 km, from the foot of the tower, then tanθ is equal to
A190B191C110D19
A flag - staff of 10 meters high stands on a building of 50 meters height.For an observer at a height of 60 meters,the flag - staff and the building subtend equal angles. The distance of the observer from the top of the flag - staff is
View SolutionRamesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it) (see the figure). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.
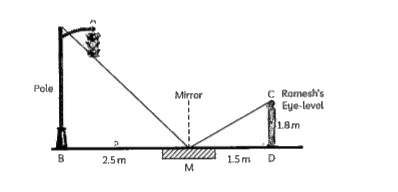
If Ramesh's eye level is 1.2 m above the ground, then the height of the pole is:
View SolutionRamesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it) (see the figure). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.
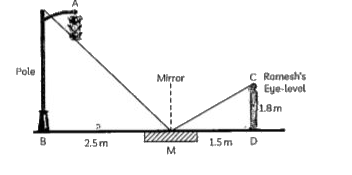
The two similar triangles shown in the figure are:
View SolutionRamesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.
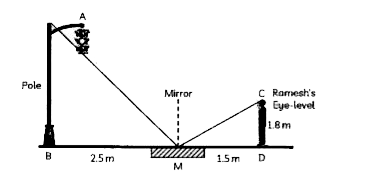
If Ramesh's eye level is 1.2 m above the ground, then the height of the pole is:
View SolutionRamesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.

If the distance of Ramesh and the pole from the mirror are 2.5 m and 1.5 m respectively, then the height of the pole is:
View Solution
