सिद्ध कीजिए की (sin4θ−cos4θ+1)cosec2θ=2 है |
The correct Answer is:दायाँ पक्ष
Step by step video, text & image solution for सिद्ध कीजिए की (sin^(4)theta-cos^(4) theta+1)"cosec"^(2) theta=2 है | by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिकोणमिति का परिचय और उसके अनुप्रयोग BOOK - NCERT EXEMPLAR HINDICHAPTER - त्रिकोणमिति का परिचय और उसके अनुप्रयोग EXERCISE - प्रश्नावली 8.1
15 Videos
- त्रिकोणमिति का परिचय और उसके अनुप्रयोग BOOK - NCERT EXEMPLAR HINDICHAPTER - त्रिकोणमिति का परिचय और उसके अनुप्रयोग EXERCISE - प्रश्नावली 8.2
12 Videos
- त्रिभुज BOOK - NCERT EXEMPLAR HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 6.4
18 Videos
Similar Questions
यदि cosA=45 है, तो tanA का मान है
View Solutiontan47∘cot43∘=1 है।
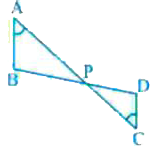
View Solutionआकृति 6.16 में, यदि ∠A=∠C,AB=6cm,AP=12cm,BP=15cm, और CP = 4 cm है, तो PD और CD की लंबाइयाँ ज्ञात कीजिए।
View Solution(sin4θ−cos4θ+1)cosec2θ का मान ज्ञात कीजिए.
View SolutionWhat is the value of (sin4θ−cos4θ+1)cosec2θ?
View Solutionयदि cosθ=√32,तो सिद्ध करें कि 3sinθ−4sin3θ=1
View SolutionProve that :
(sin4θ−cos4θ+1)cosec2θ=2
View Solutionसिद्ध कीजिए कि -
1+sinθ1+cosθ+1−sinθ1−cosθ=2cosecθ(cosecθ−cosθ)
View Solutionयदि sinθ+cosθ=x, तो सिद्ध कीजिए कि sin6θ+cos6θ=1−34(x2−1)2,x2≤2
View Solution∣∣∣4sin2θcos2θ3sec2θcosec2θ∣∣∣=
View Solutionsin4θ+2sin2θ(1−1cosec2θ)+cos4θ=
View Solutionयदि sinθ+cosecθ=2 हो, तो sin4θ+cosec4θ का मान 24 होगा |
View Solutiontan2θtan2θ−1+cos2θsin2θ−cos2θ=1sin2θ−cos2θ=tan2θtam2θ−1+cosec2θsec2θ−cosec2θ
View SolutionProve that :
(sin4θ−cos4θ+1)cosec2θ=2
View SolutionProve each of the following identities : '(i) sin^(2)theta + cos^(4) theta = cos^(2) theta + sin^(4) theta <br> (ii) "cosec"^(4) theta - "cosec"^(2) theta = cot^(4) theta + cot^(2) theta
View Solutionनिम्नलिखित सर्व समिकाओ को सिद्ध करो-
(i) (1−cosθ)(1+cosθ)(1+cot2θ)=1
(ii) (1+sinθ)2+(1−sinθ)2)2cos2θ=1+sinθ21−sin2θ
(iii) cos2θ(1−cosθ)sin2θ(1−sinθ)=1+sinθ1+cosθ
(iv) (sinθ−cosθ)2=1−2sinθ.cosθ
(v) (sinθ+cosθ)2+(sinθ−cosθ)2=2
(vi) (asinθ+bcosθ)2+(acosθ−bsinθ)2=a2+b2
(vii) cos4A+sin4A+2sin2A.cos2A=1
(ix) (cos4θ−sin4θ)=cos2θ−sin2θ=2cos2θ−1
(x) 2cos2θ−cos4θ+sin4θ=1
(xi) 1−2cos2θ+cos4θ=sin4θ
(xii) 1−2sin2θ+sin4θ=cos4θ
View Solution
