सन 1959 में लाइटलेटन एवं बॉण्डी ने सुझाया कि यदि द्रव्य पर कोई नेट आवेश हो तो विश्व (यूनिवर्स), के प्रसरण की व्याख्या की जा सकती है। जिनका संख्या घनत्व N है और जिसे और जिसे नियत रखा जाता है, मान लीजिए प्रोटॉन पर आवेश ep=−(1+y)e है, यहाँ e इलेक्ट्रॉनिक आवेश है।
(a) y का वह क्रांतिक मान ज्ञात कीजिए, जिस पर प्रसरण आरम्भ हो सके।
(b) यह दर्शाइए कि प्रसरण का वेग केन्द्र से दूरी के वर्ग के अनुक्रमानुपाती है।
मान लीजिए विश्व की त्रिज्या R है। यह मानिए कि हाइड्रोजन परमाणु एकसमान रूप से वितरित है। प्रत्येक हाइड्रोजन परमाणु पर आवेश eH=−(1+y)e+e=−ye=|ye|
प्रत्येक हाइड्रोजन परमाणु का द्रव्यमान प्रोटॉन के द्रव्यमान ~mp के तुल्य है। जब R पर, किसी हाइड्रोजन परमाणु पर यदि कूलॉम-प्रतिकर्षण गुरुत्वीय आकर्षण से अधिक हो जाए तो विस्तार आरम्भ हो जाता है।
मान लीजिए R पर विद्युत क्षेत्र E है, तब
4πR2E=43ε0πR2N|ye| (गाउस नियम)
E(R)=13N|ye|εoR→r
मान लीजिए R पर गुरुत्वीय क्षेत्र GR है।
−4πR2GR=4πGmp43πR3N
GR=−43πGmρNR
GR(R)=−43πGmρNRˆr
इस प्रकार R पर हाइड्रोजन परमाणु पर कूलॉम-बल है
yeE(R)=13Ny2e2εoRˆr
इस परमाणु पर गुरुत्वाकर्षण बल है
mpGR(R)=−4π3GNm2pRˆr
परमाणु पर नेट बल है
F=(13Ny2e2εoR−4π3GNm2pR)ˆr
यह क्रांतिक मान तब है जब
13Ny2ce2εoR=4π3GNm2pR
=y2c=4πεoGm2pe2
≅7×10−11×1.82×106×81×10−629×109×1.62×10−38
~63×10−38
∴yc~8×10−19~10−18
(b) इस नेट बल के कारण हाइड्रोजन परमाणु किसी त्वरण का अनुभव करता है जो इस प्रकार होता है, कि
mrd2Rdt2=(13Ny2e2eoR−4p3GNm2pR)
अथवा d2Rdt2=a2R जहाँ a2=1mp(13Ny2e2eo−4p3GNm2p)
इसका एक हल R=Aeat+Be−at
चूँकि हम कोई विस्तार खोज रहे है, B=0
∴R=Aeat
⇒R=αAeat=αR
इस प्रकार वेग केन्द्र से दूरी के अनुक्रमानुपाती है।
Topper's Solved these Questions
- वैद्युत आवेश तथा क्षेत्र BOOK - NCERT EXEMPLAR HINDICHAPTER - वैद्युत आवेश तथा क्षेत्र EXERCISE - लघुउत्तरीय (SA)
6 Videos
- विद्युतचुम्बकीय प्रेरणBOOK - NCERT EXEMPLAR HINDICHAPTER - विद्युतचुम्बकीय प्रेरणEXERCISE - दीर्घउत्तरीय (LA)
10 Videos
- संचार व्यवस्थाBOOK - NCERT EXEMPLAR HINDICHAPTER - संचार व्यवस्थाEXERCISE - दीर्घउत्तरीय (LA)
11 Videos
Similar Questions
कोई सिक्का Al−Mg मिश्रातु का बना है और इसका भार 0.75g है। यह वर्गाकार है तथा इसके विकरणों की माप 17 mm है। यह वैद्युत उदासीन है तथा इसमें धन और ऋण आवेश समान मात्रा में है।
यह मानते हुए कि पैसे के सिक्के केवल Al के बने है, धन तथा ऋण आवेशों की समान संख्याओं के परिमाण ज्ञात कीजिए। इस परिमाण से आप क्या निष्कर्ष निकालते है?
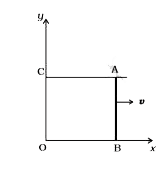
View Solutionकोई चुम्बकीय क्षेत्र B=B0sin(ωt)ˆk किसी विशाल प्रदेश पर आच्छादित है जिसमें तार AB ऐसे दो समांतर चालकों पर निर्बाध सरकता है जो एक दूसरे से d दूरी द्वारा पृथक्कृत है। ये तार x-y तल में है । तार AB (लम्बाई d की) का प्रतिरोध R है तथा समांतर चालकों (तारों) का प्रतिरोध उपेक्षणीय है। यदि AB v वेग से गमन करता है तो परिपथ में कितनी धारा है? तार को नियत वेग से गमन करने के लिए कितने बल की आवश्यकता है?
View Solutionकिसी संचार चैनल के अनुदिश गतिशील प्रकाश स्पन्द की तीव्रता, दूरी के साथ चरघातांकी रूप से, निम्न संबंध के अनुसार घटती है, I=I0e−αx जहाँ I0.x=0 पर तीव्रता है तथा α क्षीणन नियतांक है। दिखाइये कि (In4α) दूरी तय करने के पश्चात् तीव्रता में 75% की कमी आ जाती है।
View Solutionबिंदु P,Q,R,S के निर्देशांक (2,a),(3,5),(3,4)और (0,6) है । यदि रेखा PR लंबवत हो QS पर तो a का मान ज्ञात कीजिए ।
View Solutionएक छोटी फर्म सोने के अंगूठियां और चेनों का निर्माण करती है| प्रतिदिन अंगूठियों और चेनों के निर्माण की कुल संख्या अधिकतम 24 है| एक अंगूठी बनाने में एक घंटा तथा के चेन के बनाने में 30 मिनट लगते है| प्रतिदिन उपलब्ध घंटों की अधिकतम संख्या 16 है|यदि अंगूठी पर लाभ रु 300 तथा एक चेन पर लाभ रु 190 हो, तो ज्ञात कीजिए| की प्रतिदिन कितनी अंगूठियों और चेनों का निर्माण किया जाय ताकि अधिकतम लाभ कमाया जा सकें|
View Solutionस्पर्श रेखा y- अक्ष पर लंबवत हो तो dydx का मान कितना होता है ?
View Solutionमाना की R कोई वास्तविक सँख्या का समुच्चय है। एक सक्रिया R पर इस प्रकार परिभाषित है कि a*b=a+b+2ab तो 2*3 का मान ज्ञात किया।
View Solutionयदि संख्या 354Y2, 6 का एक गुणज है तो Yअंक का मान क्या हो सकता है?
View Solutionबोरेक्स में बोरॉन-ऑक्सीजन बंधों की कुल संख्या 'x' है और बोरॉन ऑक्सीजन-बोरॉन बंधों की 'y' है। तो x - y का मान है:
View Solutionबोरेक्स (Na2B4O7.10H2O) में यदि sp2 संकरित B- परमाणुओं की संख्या X है औरsp3 संकरित B- परमाणुओं की संख्या Y है। तो X+Y के योग का मान क्या है?
View SolutionXeO_(3)F_(2) में XE( केंद्रीय परमाणु) पर बंध युग्मों की संख्या X और एकांकी युग्मों की संख्या Y है। तो X+Y का योग क्या है?
View Solutionदो द्रवों A और B के एक आदर्श मिश्रण को पिस्टन युक्त एक सिलेण्डर में रखा जाता है। पिस्टन को समतापीय रूप से खीचने पर द्रव का आयतन घटता है लेकिन वाष्प का आयतन बढ़ जाता है। द्रव की बहुत छोटी मात्रा शेष बचती है और वाष्प में A का मोल प्रभाज 0.4 होता है। यदि प्रायोगिक ताप पर P_(A)^(@) = 0.4 और P_(B)^(@) = 1.2 atm है, तो निम्नलिखित में से किस कुल दाब पर द्रव लगभग वाष्पीकृत हो जाता है?
View Solutionयहाँ दिए गए यौगिक में,
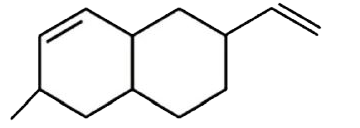 यदि X और Y क्रमश: द्वितीयक और तृतीयक C परमाणुओं की संख्या है। यहाँ x+Y के योगफल का मान ज्ञात कीजिए।
यदि X और Y क्रमश: द्वितीयक और तृतीयक C परमाणुओं की संख्या है। यहाँ x+Y के योगफल का मान ज्ञात कीजिए।
View Solutionयदि Mn2+ में अयुग्मित इलेक्ट्रॉनों की संख्या 'X' है और +2 की तुलना में अन्य धनात्मक ऑक्सीकरण अवस्था 'Y' है। यहाँ x + Y का योग क्या है|
View Solution298 K पर N_(2) गैस की जल में विलेयता के लिए हेनरी नियम का स्थिरांक 1xx10^(-5) atm है। वायु में N_(2) का मोल प्रभाज 0.8 है। यदि 298 K और 5 atm पर जल के 10 मोल में विलेय वायु के N_(2) के मोलों की संख्या x*10^(-4) है, तो x का मान ज्ञात कीजिए।
View Solutionताप T पर एक प्रतिदर्श में N_2 अणुओं की वर्ग माध्य मूल गति 'x' है। यदि ताप को दोगुना किया जाता है, तो नाइट्रोजन के अणु, परमाणुओं में वियोजित हो जाते हैं, और नाइट्रोजन परमाणुओं की वर्ग माध्य मूल गति 'x' की n गुना हो जाती है। यहाँ n का मान ज्ञात कीजिए।
View Solution
