Three rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
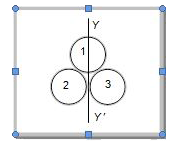
3MR2
32MR2
5MR2
72MR2
The correct Answer is:D
M.I of system about YY. I=I1+I2+I3
where I1 = moment of inertia of ring about diameter l2=l3 = M.I. of inertia of ring about a tangent in a plane
∴I=12mR2+32mR2+32mR2=72mR2
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on centre of mass)
12 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on angular displacement, velocity and acceleration)
16 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
Knowledge Check
Three rings each of mass M and radius R are arranged as shown in the figure . The moment of inertia of the system about AB is
(NAR_NEET_PHY_XI_P2_C07_E11_036_Q01.png" width="80%">A3Mr2B32MR2C5MR2D72MR2Three rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be
 A72PQ2B27PQ2C25PQ2D52PQ2
A72PQ2B27PQ2C25PQ2D52PQ2Three point masses are arranged as shown in the figure. Moment of inertia of the system about the axis OO' is
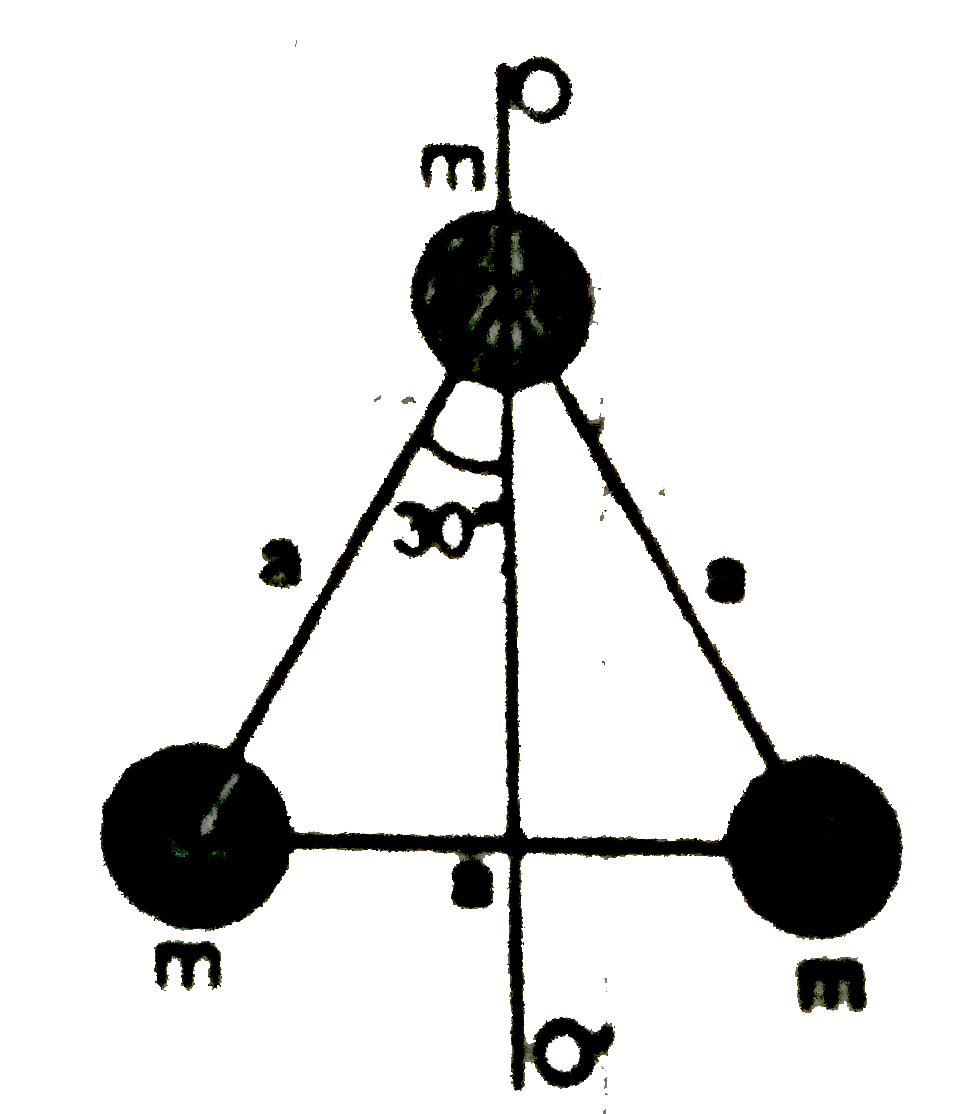 A2ma2Bma22Cma2Dnone of these
A2ma2Bma22Cma2Dnone of these
Three identical solid discs, each of mass M and radius R, are arranged as shown in figure. The moment of inertia of the system about an axis AB will be

View SolutionThree rings each of mass M and radius R are arranged according to the figure. The moment of inertia of this system about an axis XX' on its plane would be

View SolutionThree rings each of mass M and radius R are placed in contact with each other as shown . Then MI of the system about YY' axis is

View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
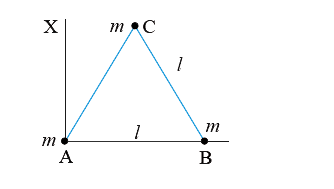
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View SolutionTwo identical concentric rings each of mass m and radius R are placed perpendicularly. What is the moment of inertia of the system about the axis of one of the rings ?
View Solution


