In a playground there is a merry-go-round of mass 120 kg and radius 4 m. The radius of gyration is 3m. A child of mass 30 kg runs at a speed of 5 m/sec tangent to the rim of the merry-go-round when it is at rest and then jumps on it. Neglect friction and find the angular velocity of the merry-go-round and child
0.2 rad/sec
0.1 rad/sec
0.4 rad/sec
0.8 rad/sec
The correct Answer is:C
To solve the problem, we will use the principle of conservation of angular momentum. The total angular momentum before the child jumps onto the merry-go-round must equal the total angular momentum after the child has jumped on.
1. Identify the given values:
- Mass of the merry-go-round, M=120kg
- Radius of the merry-go-round, R=4m
- Radius of gyration of the merry-go-round, k=3m
- Mass of the child, m=30kg
- Speed of the child, v=5m/s
2. Calculate the moment of inertia of the merry-go-round:
The moment of inertia I of the merry-go-round can be calculated using the formula:
I=Mk2
Substituting the values:
I=120kg×(3m)2=120×9=1080kg⋅m2
3. Calculate the angular momentum of the child before jumping on the merry-go-round:
The angular momentum L of the child can be calculated using the formula:
L=m⋅v⋅R
Substituting the values:
L=30kg×5m/s×4m=600kg⋅m2/s
4. Total initial angular momentum:
Since the merry-go-round is initially at rest, its initial angular momentum is 0. Therefore, the total initial angular momentum is:
Linitial=600kg⋅m2/s
5. Calculate the total moment of inertia after the child jumps on the merry-go-round:
The moment of inertia of the child when he is on the merry-go-round is given by:
Ichild=m⋅R2
Substituting the values:
Ichild=30kg×(4m)2=30×16=480kg⋅m2
Therefore, the total moment of inertia after the child jumps on is:
Itotal=I+Ichild=1080kg⋅m2+480kg⋅m2=1560kg⋅m2
6. Apply conservation of angular momentum:
The total angular momentum after the child jumps on is given by:
Lfinal=Itotal⋅ω
Setting the initial and final angular momentum equal:
600=1560⋅ω
Solving for ω:
ω=6001560=1539=513≈0.3846rad/s
Final Answer:
The angular velocity of the merry-go-round and the child after the child jumps on is approximately 0.3846rad/s.
- Mass of the merry-go-round, M=120kg
- Radius of the merry-go-round, R=4m
- Radius of gyration of the merry-go-round, k=3m
- Mass of the child, m=30kg
- Speed of the child, v=5m/s
The moment of inertia I of the merry-go-round can be calculated using the formula:
I=Mk2
Substituting the values:
I=120kg×(3m)2=120×9=1080kg⋅m2
The angular momentum L of the child can be calculated using the formula:
L=m⋅v⋅R
Substituting the values:
L=30kg×5m/s×4m=600kg⋅m2/s
Since the merry-go-round is initially at rest, its initial angular momentum is 0. Therefore, the total initial angular momentum is:
Linitial=600kg⋅m2/s
The moment of inertia of the child when he is on the merry-go-round is given by:
Ichild=m⋅R2
Substituting the values:
Ichild=30kg×(4m)2=30×16=480kg⋅m2
Therefore, the total moment of inertia after the child jumps on is:
Itotal=I+Ichild=1080kg⋅m2+480kg⋅m2=1560kg⋅m2
The total angular momentum after the child jumps on is given by:
Lfinal=Itotal⋅ω
Setting the initial and final angular momentum equal:
600=1560⋅ω
Solving for ω:
ω=6001560=1539=513≈0.3846rad/s
The angular velocity of the merry-go-round and the child after the child jumps on is approximately 0.3846rad/s.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on kinetic energy, work and power)
30 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on rolling on incline plane)
28 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on moment of inertia)
33 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
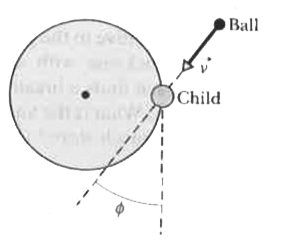
In Fig. 10-86, a 30 kg child stands on the edge of a stationary merry-go-round of radius 2.0 m. The rotational inertia of the merry-go-round about its rotation axis is 150kg⋅m2. The child catches a ball of mass 1.0 kg thrown by a friend. Just before the ball is caught, it has a horizontal velocity →v of magnitude 12 m/s, at angle ϕ=37∘ with a line tangent to the outer edge of the merry-go-round, as shown. What is the angular speed of the merry-go-round just after the ball is caught?
View SolutionThree schoolboys, Sam, John, and Nick, are on merry-go-round. Sam and John occupy diametrically opposite points on a merry-go-round of radius r. Nick is on another merry-go-round of radius R. The positions of the boys at the initial instant are shown in Fig. Considering that the merry-go-round touch each other and rotate in the same direaction at the same angular velocity ω, determine the nature of motion of Nick from John's point of view and of Sam from Nick's point of view.

View Solution
Knowledge Check
A playground merry-go-round is at rest, pivoted about a frictionless axis. A child of mass m runs along a path tangential to the rim with speed v and jumps on to the merry-go-round. If R is the radius of the merry-go-round and I is its moment of inertia, then the angular velocity of the merry-go-round is
AmvRmR2+IBmvRICmR2mvRDImvRA child is standing on the edge of a merry-go-round that has the shape of a disk, as shown in the figure. The mass of the child is 40 kg. The merry-go-round has a mass of 200kg and a radius of 2.5 m, and it is rotating with an angular velocity of ω=2.0 radians per second. The child then walks slowly towards the centre of the merry-go-round. What will be the final angular velocity of the merry-go-round when the child reaches the centre? (The size of the child can be neglected)
 A2.0 rad/sB2.2 rad/sC2.4 rad/sD2.8 rad/s
A2.0 rad/sB2.2 rad/sC2.4 rad/sD2.8 rad/sa body of mass 10 kg and radius of gyration 0.1 m is rotating about an axis. If angular speed is 10 rad/s, then angular momentum will be:
A1kgm2/sB0.1kgm2/sC100kgm2/sD10kgm2/s
A body of mass 2 kg and radius of gyration 0.5 m is rotating about an axis. If its angular speed is 2 rad/s, then the angular momentum of the body will be
View Solution
A child with mass m is standing at the edge of a merry go round having moment of inertia I, radius R and initial angular velocity ω as shown in the figure. The child jumps off the edge of the merry go round with tangential velocity v with respect to the ground. The new angular velocity of the merry go round is
View SolutionA girl of mass M stands on the rim of a frictionless merry-go-round of radius R and rotational inertia I that is not moving. She throws a rock of mass m horizontally in a direction that is tangent to the outer edge of the merry-go-round. The speed of the rock, relative to the rock. relative to the ground, is v. After, the linear speed of the girl is.
 .
.
View SolutionA playground merry-go-round of radius R=2.00 has a moment of inertia I=250kg.m2 and is rotating 10.0rev/min about a frictionless, vertical axle. Facing axle, a 25.0−kg child hops onto the merry-go-round and manages to sit down on the edge. The new angular speed of the merry-go-round is.
View SolutionA wheel of mass 40 kg and radius of gyration 0.5 m comes to rest from a speed of 180 rpm in 30 s assuming that the retardation is uniform then the value of the retarding torque, in Nm will be
View Solution
