(i) एक स्रोत (S) तथा एक प्रेक्षक (O) के बीच रखे एक लेंस पर विचार कीजिए (चित्र 9.8)। मान लीजिए लेंस की मोटाई w(b)=w0−b2α के अनुसार बदलती है, जहाँ b प्रकाशिक केन्द्र से ऊर्ध्वाधर दूरी है, w0 एक नियतांक है। फरमैट के सिद्धान्त (अर्थात किसी किरण के लिए स्रोत तथा प्रेक्षक के बीच पारगमन का समय चरममान होता है) का उपयोग करके शर्त ज्ञात कीजिए कि स्रोत से प्रारम्भ होने वाली सभी उपाक्षीय किरणें अक्ष के बिन्दु O पर अभिसरित होंगी। लेंस की फोकस दूरी भी ज्ञात कीजिए।
(ii) गुरुत्वीय लेंस को निम्नलिखित सूत्रानुसार बदलती हुई मोटाई का माना जा सकता है :
w(b)=k1ln(k2b) bmin<b<bmax
=k1ln(k2bmin)b<bmin
दर्शाइए कि कोई प्रेक्षक बिंदु-बिंब के प्रतिबिंब को लेंस के केन्द्र के गिर्द एक वलय के रूप में देखेगा जिसकी कोणीय त्रिज्या होगी -
β=√(n−1)k1uvu+v

(i) S से P1तक पारगमन का समय है
t1=SP1c=√u2+b2c≅uc(1+12b2u2) मान लीजिए b<<u0
P1 से O तक पारगमन का समय है
t2=P1Oc=√v2+b2c≅vc(1+12b2v2)
लेंस से पारगमन का समय है
t1=(n−1)w(b)cजहाँ n अपवर्तनांक है।
अतः कुल समय है
t=1c[u+v+12b2(1u+1v)+(n−1)w(b)]⋅1D=1u+1v रखिए
तब t=1c(u+v+12b2D+(n−1)(w0+b2α))
फरमैट के सिद्धांत से
dtdb=0=bXD−2(n−1)bcα
α=2(n−1)D
अत: यदि α=2(n−1)Dतो अभिसरणकारी लेंस बनेगा। यह b से स्वतन्त्र है और इसलिए S से आने वाली सभी उपाक्षीय किरणें O पर अभिसरित होंगी (अर्थात b<<n तथा b<<v किरणों के लिए)।
क्योंकि 1D=1u+1v,फोकस दूरी है।
(ii) इस स्थिति में
t=1c(u+v+12b2D+(n−1)k1 in (k2b))
dtdb=0=bD−(n−1)k1b
⇒b2=(n−1)k1D
∴b=√(n−1)k1D
अत: ऊँचाई से गुजरने वाली सभी किरणें प्रतिबिंब बनाने में योगदान देंगी। किरण पथ द्वारा बनाया गया कोण
β≅bv=√(n−1)k1Dv2=√(n−1)k1uvv2(u+v)=√(n−1)k1u(u+v)v

Topper's Solved these Questions
- किरण प्रकाशिकी एवं प्रकाशिक यंत्र BOOK - NCERT EXEMPLAR HINDICHAPTER - किरण प्रकाशिकी एवं प्रकाशिक यंत्र EXERCISE - लघुउत्तरीय (SA)
6 Videos
- अर्धचालक इलेक्ट्रोनिकी- पदार्थ, युक्तियाँ तथा सरल परिपथBOOK - NCERT EXEMPLAR HINDICHAPTER - अर्धचालक इलेक्ट्रोनिकी- पदार्थ, युक्तियाँ तथा सरल परिपथEXERCISE - दीर्घउत्तरीय
10 Videos
- गतिमान आवेश और चुम्बकत्व BOOK - NCERT EXEMPLAR HINDICHAPTER - गतिमान आवेश और चुम्बकत्व EXERCISE - दीर्घउत्तरीय (LA)
7 Videos
Similar Questions
किसी अवतल दर्पण के मुख्य अक्ष के अनुदिश फोकस से दूर, L लम्बाई का एक छोटा बिंब रखा गया है। बिंब की दूरी v है। यदि दर्पण की फोकस दूरी f है तो प्रतिबिंब की लम्बाई कितनी होगी? आप L<<|v−f| मान सकते हैं।
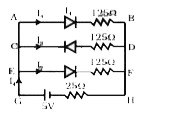
View Solutionयदि चित्र में दर्शाए गए प्रत्येक डायोड का अग्रबायस प्रतिरोध 25Ω तथा पश्च बायस प्रतिरोध अनन्त हो, तो धारा I1,I2,I3 एवं I4 के मान क्या होंगे?
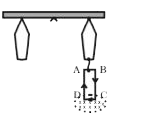
View Solution100 फेरों की कोई आयताकार कुण्डली ABCD (XY तल में) तुला की एक भुजा से लटकी है (चित्र 4.4)। कुण्डली का भार संतुलित करने के लिए दूसरी भुजा पर 500g बाट रखा गया है। अब कुण्डली से 4.9A धारा प्रवाहित की जाती है तथा भीतर की ओर (XZ तल में) कार्यरत 0.2 T का नियत चुम्बकीय क्षेत्र इस प्रकार लगाया जाता है कि केवल CD भुजा जिसकी लम्बाई 1 cm है, कुण्डली क्षेत्र में रहे। तुला पर कितना अतिरिक्त द्रव्यमान .m. रखें कि पुनः संतुलन प्राप्त हो जाए?
View Solutionनिम्नलिखित प्रश्नो के उत्तर दीजिए :
अहिंसा एक विज्ञान है इस विचार का पाठ के आधार पर विवेचना कीजिए ।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionएक अनभिनत पासे को 5 बार उछाला जाता है एक समसंख्या प्राप्त करना एक सफलता है तो प्रायिकता ज्ञात कीजिए - अधिक से अधिक 4 सफलताओ के लिए
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। प्रायिकता ज्ञात कीजिए कि 5 कदम चलने के पश्चात, यह व्यक्ति प्रारम्भिक बिन्दु से एक कदम दूर है।
View Solutionएक चतुष्फलक के चारो शीर्ष O(0,0,0), A(1,2,1),B(2,1,3) और C(-1,1,2) है चतुफलक का आयतन ज्ञात कीजिए।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solution
