हाइड्रोजन परमाणु का बोर मॉडल स्थिर विद्युत के कूलॉम-नियम पर निर्भर करता है। कूलॉम का नियम प्रत्यक्षतः बहुत अल्प दूरियों (Å के समकक्ष) के लिए परीक्षित नहीं है। माना कूलॉम का नियम दो विपरीत आवेशों +q1,−q2 के लिए परिष्कृत किया गया है-
|F|=q1q2(4πε0)1r2,r≥R0
=q1q24πε01R20(R0r)ε,r≤R0
इस स्थिति में H-परमाणु की न्यूनतम ऊर्जा अवस्था का परिकलन कीजिए, यदि epsi= 0.1 , R_0 = 1 Å |
माना ε=2+δ
F=q1q24πε0,Rδ0r2+δ=∧Rδ0r2+δ, जहाँ q1q24π0ε=∧,∧=(1.6×10−19)2×9×10−9
=23.04×10−29
=mv2r
u2=∧Rδ0mr1+δ
(i) mvr=nh,r=nhmv=mhm[m∧Rδ0]1/2r(1/2+δ/2)
इसे r के लिए हल करने पर rn=[n2h2m∧Rδ0]11−δ
n= 1 के लिए, तथा स्थिरांक के मान रखने पर, हमें प्राप्त होता है r1=[h2m∧Rδ0]11−δ
r1=[1.052×10−689.1×10−31×2.3×10−28×10+19]12.9=8×10−11=0.07nm
(<0.1nm)
(ii) vn=nhmrn=hn(m∧Rδ0n2h2)11−δn=1के लिए ,v1=hmr1=1.44×106 m/s
गतिज उर्जा =12mv21=9.43×10−19J=5.9eV
स्थितिज ऊर्जा R0 का =∧R0
R0 से r एक स्थितिज ऊर्जा =+∧Rs0∫rR0drr2+δ+∧Rs0−1−δ[1r1+δ]rR0
=−∧Rδ01+δ[1r1+δ−1R1+δ0]तक
स्थितिज ऊर्जा =−(∧1+δ)[Rs0r1+δ−1R0]
=−∧1+δ[Rs0r1+δ−1R0+1+δR0]
=∧−0.9[R−1.90r−0.9−1.9R0] =2.30.9×10−18[(0.8)0.9−1.9]J=−17.4eV
कुल ऊर्जा है (−17.3+5.9]=−11.4eV
Topper's Solved these Questions
Similar Questions
पोजीट्रोनियम, पोज़ीट्रॉन (इलेक्ट्रॉन का धनात्मक रूप से आवेशित वह प्रतिकण जो इलेक्ट्रॉन के समान ही द्रव्यमान वाला होता है) के द्वारा विस्थापित प्रोटॉन वाले H-परमाणु के समान होता है। पोजीट्रोनियम की मूल अवस्था ऊर्जा होगी-
View Solutionकभी-कभी कोई रेडियोएक्टिव नाभिक विघटित होकर एक ऐसा नाभिक बनाता है जो स्वयं भी रेडियोएक्टिव होता है, उदाहरणार्थ 38Sअधायु −−−−→=2.48h38Cl अधायु −−−−→=0.2h38Ar (स्थायी) मान लीजिए हम 1 = 0 पर 1000 S18 नाभिकों से प्रारम्भ करते हैं। 1 = 0 पर 38CI की संख्या शून्य है तथाt=∞ पर पुन: शून्य है। 1 के किस मान पर नाभिकों की संख्या अधिकतम होगी और उस समय यह संख्या क्या होगी?
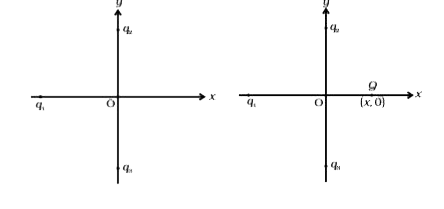
View Solutionचित्र 1.1 में y-अक्ष के अनुदिश स्थित दो वैद्युत आवेश q2 तथा q3 , X-अक्ष के अनुदिश स्थित वैद्युत आवेश q1 पर, +x दिशा में कोई नेट विद्युत बल आरोपित करते हैं। यदि (x, 0), पर कोई धनावेश Q रख दिया जाए तो q1 पर आरोपित बल
View Solutionकूलॉम से पहले|कूलॉम के नियम|कूलॉम के नियम पर कुछ प्रश्न|OMR
View Solutionकूलॉम के नियम महत्वपूर्ण प्रश्न|OMR|Summary
View Solutionगेलुसाक का नियम आवोगाद्रो का नियम डाल्टन का परमाणु सिद्धांत|रासायनिक संयोजन के नियम|Summary
View Solutionकूलॉम का नियम
View Solutionकूलॉम का नियम |कूलॉम के नियम का सदिश रूप |OMR|Summary
View Solutionआवेशों के लिए अध्यारोपण का सिद्धांत#!#कूलाम्ब के नियम पर आधारित प्रशन
View Solutionकूलॉम का नियम
View Solutionकूलॉम के नियम का सदिश रूप | माध्यम में कूलॉम का नियम
View Solutionहाइड्रोजन परमाणु के लिए बोर मॉडल |Summary
View Solutionहाइड्रोजन परमाणु के लिए बोर मॉडल |प्रश्न|H परमाणु में विभिन्न कोश की ऊर्जा|Summary
View Solutionहाइड्रोजन परमाणु के द्वितीय बोर कक्षा में एक इलेक्ट्रॉन की गतिज ऊर्जा है- [ a_(0) हाइड्रोजन परमाणु के प्रथम कोश की बोर त्रिज्या है]
View Solutionनाभिक से दूरी पर, अनंतसूक्ष्म मोटाई dr के गोलीय कोश में हाइड्रोजन परमाणु के 1s इलेक्ट्रॉन के पाए जाने की प्रायिकता P है। इस कोश का आयतन 4rr2 dr है। r पर P की निर्भरता का गुणात्मक रेखाचित्र है-
View Solution
