P is the centre of mass of a system of four point masses A,B,C and D, which are coplanar but not collinear.
(a) P may or may not coincide with one of the point masses
(b) P must lie within or on the edge of atleast one of the triangles formed by taking A,B, C and D three at a time
(c ) P must lie on a line joining two of the points A,B,C,D
(d ) P lies out side the quadrangle ABCDSolution in Telugu
a & b are correct
c & d are correct
a & c are correct
b & d are correct
The correct Answer is:A
Step by step video, text & image solution for P is the centre of mass of a system of four point masses A,B,C and D, which are coplanar but not collinear. (a) P may or may not coincide with one of the point masses (b) P must lie within or on the edge of atleast one of the triangles formed by taking A,B, C and D three at a time (c ) P must lie on a line joining two of the points A,B,C,D (d ) P lies out side the quadrangle ABCD by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Exercise-II109videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE99videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Problems103videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )8videos
SURFACE TENSION
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions2videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Centre of mass of two particle with masses 2 kg and 1 kg locsted at (1, 0, 1) and (2, 2, 0) has the co - ordinates of
05:16View SolutionThe centre of mass of two particles with masses 2kg and 6 kg located at (1,1,1), (2,2,1) respectively has the coordinates
03:39View SolutionIf the distance between the centres of the atoms of potassium and bromine in KBr (potassium - bromide) molecule is 0.282×10−9m, find the centre of mass of this particle system from potassium (mass of bromine = 80 u, and of potassium = 39 u).
07:37View SolutionIf the work done in blowing a soap bubble of volume 'V' is W, then the work done in blowing a soap bubble of volume '2V' is
04:18View SolutionA constant pressure gas thermometer has a volume of 200cc, 273.2cc and 525 .1cc at 0°C, 100°C and boiling point of sulphur respectively. The resistance possessed by a platinum wire at the same temperatures as above are 2.000Ω,2.778Ωand5.280Ω respectively. Estimate the boiling point of sulphur on the basis of the two sets of observations.
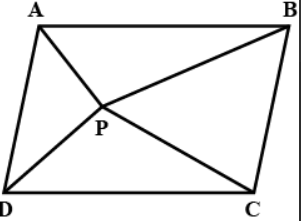
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
 02:00View Solution
02:00View SolutionTwo triangle ABC and DBC lie on the same side of the base BC . From a point P on BC,PQAB AND PRBD ARE DRAWN. They meet AC in Q and DC in R respectively. Prove that QRAD.
04:27View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)
 11:49View Solution
11:49View SolutionP is the centre of mass of four point masses A,B, C and D which are lying in the same length but not along the same straight line then.
02:43View SolutionIn three dimensions there may be more than one point, which are equidistant from three given non-collinear points A, B, C. One of these points will be circumcentre of the triangle ABC.
The y-coordinate of the circumcentre of triangle ABC must be09:21View SolutionCalculate centre of mass of the system
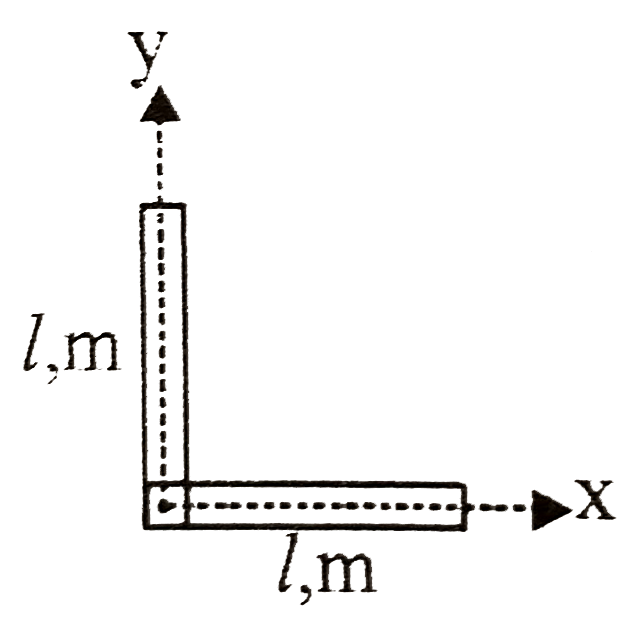 06:28View Solution
06:28View SolutionFor positive real numbers a,bc such that a+b+c=p, which one holds? (a) (p−a)(p−b)(p−c)≤827p3 (b)(p−a)(p−b)(p−c)≥8abc (c)bca+cab+abc≤p (d) none of these
09:19View SolutionABCD are four points in a plane and Q is the point of intersection of the lines joining the mid-points of AB and CD;BC and AD. Show that →PA+→PB+→PC+→PD=4→PQ, where P is any point.
05:32View SolutionABCD is a parallelogram. P is a point on AD such that AP=13AD and Q is a point on BC such that CQ=13BP . Prove that AQCP is a parallelogram.
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
05:44View Solution

