A heavy wheel of radius 20 cm and weight 10kg is to be dragged over a step of height 10cm, by a horizontal force F applied at the centre of the wheel. The minimum value of F is
20 kgwt
1 kgwt
10√3 kgwt
10√2 kgwt
The correct Answer is:C
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - II) Torque, toppling (More than One correct answer Type Questions)
4 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - II) Torque, toppling (Linked Comprehention Type Questions)
5 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LECTURE SHEET (EXERCISE - I) Moment of Inertia ( Integer Type Questions )
2 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
As shown, a wheel of weight W and radius 1.0m is placed against a 0.4m height rectangular block fixed on the ground. The wheel has an axle of radius 0.1m. A force F is applied tangentially to the axle to lift the wheel. The minimum value of F is given.by expression F=αW11. Then find the value of α.
'(##CEN_KSR_PHY_JEE_C09_E01_039_Q21##)'
View SolutionA cuboid of height 10 cm, width 5 cm and 8 kg is kept on a rough horizontal ground as shown . The ground is so rough that we can assume that the questions indicated below. A boy applies a horizontal force F at the top edge of the cuboid.

What is the minimum value of F so taht the block begins to topple ?
View Solution
Knowledge Check
A heavy wheel of radius 20cm and weight 10kg is to be dragged over a step of height 10cm, by a horizontal force F applied at the centre of the wheel. The minimum value of F is
A20kgwtB1kgwtC10√3kgwtD10√2kgwtA wheel of radius r and mass m stands in front of a step of height h. The least horizontal force which should be applied to the axle of the wheel to allow it to raise onto the step is
 Amgh(2r−h)r−hBmgh(r−h)Cmg(√h(2r−h))r−hDmghr
Amgh(2r−h)r−hBmgh(r−h)Cmg(√h(2r−h))r−hDmghrA roller of mass 300kg and of radius 50cm lying on horizontal floor is resting against a step of height 20cm. The minimum horizontal force to be applied on the roller passing through its centre to turn the roller on to the step is
A980NB1960NC2940ND3920N
A uniform cylinder of mass M and radius R is to be pulled over a step of height a (a<R) by applying a force F at its centre O perpendicular to the plane through the axes of the cylinder on the edge of the step (see figure ) . The minimum value of F required is :

View SolutionA uniform cylinder of mass M and radius R is to be pulled over a step of height a (a<R) by applying a force F at its centre O perpendicular to the plane through the axes of the cylinder on the edge of the step (see figure ) . The minimum value of F required is :

View SolutionThe drwing shows a bicycle wheel of radius r, resting against a small step whose height is h=r/5. A clockwise torque increases, there comes a time when the wheel just begins to rise up and loses contact with the ground. Let this torque be T. What is the magniitude of the horizontal component of the acceleration of the centre of the wheel when a torque of 2T is applied? Assume that the wheel doesn't slip at the edge of the step when this torque is applied (ignore the mass of the spokes).

View SolutionThe minimum horizontal force applied to the centre of wheel of radius R and weight w to pull it over a step of height R/2
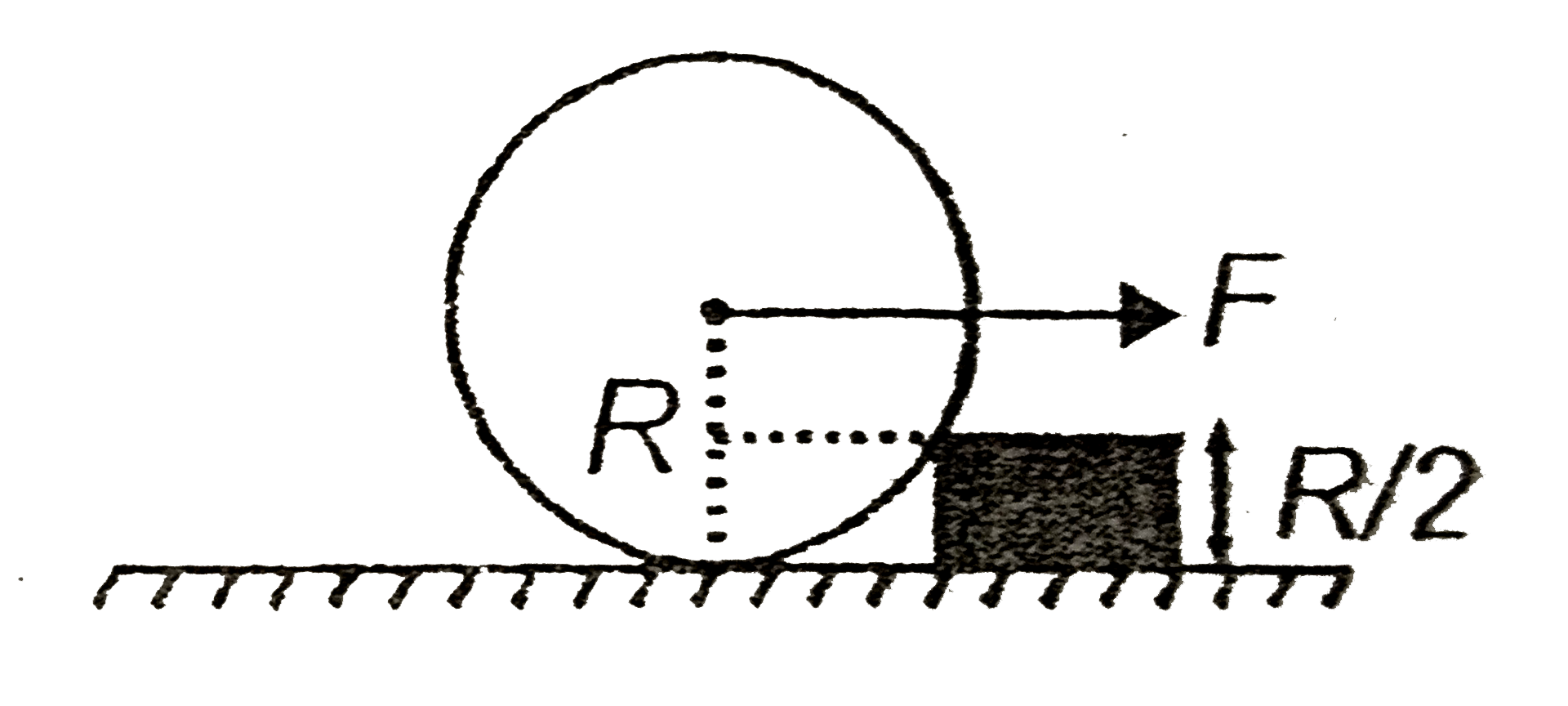
View SolutionThe drwing shows a bicycle wheel of radius r, resting against a small step whose height is h=r/5. A clockwise torque increases, there comes a time when the wheel just begins to rise up and loses contact with the ground. Let this torque be T. What is the magniitude of the horizontal component of the acceleration of the centre of the wheel when a torque of 2T is applied? Assume that the wheel doesn't slip at the edge of the step when this torque is applied (ignore the mass of the spokes).

View Solution
