Three particles A,B,C of mass m each are joined to each other by massless rigid rods to form an equilateral triangle of side a. Another particle of mass m hits B with a velocity v0 directed along BC as shown. The colliding particle stops immediately after impact.n The time required by the triangle ABC to complete half revoution in its subsequent motion is xaπ√3V0 where 'x' is

The correct Answer is:6
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - IV) (LEVEL - I Straight Objective Type Questions)
26 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - IV) (LEVEL - II Straight Objective Type Questions)
4 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - III) (LEVEL - II More than One correct answer Type Questions)
5 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
Three particles A,B,C of mass m each are joined to each other by massless rigid rods to form an equilateral triangle of side a. Another particle of mass m hits B with a velocity v0 directed along BC as shown. The colliding particle stops immediately after impact.
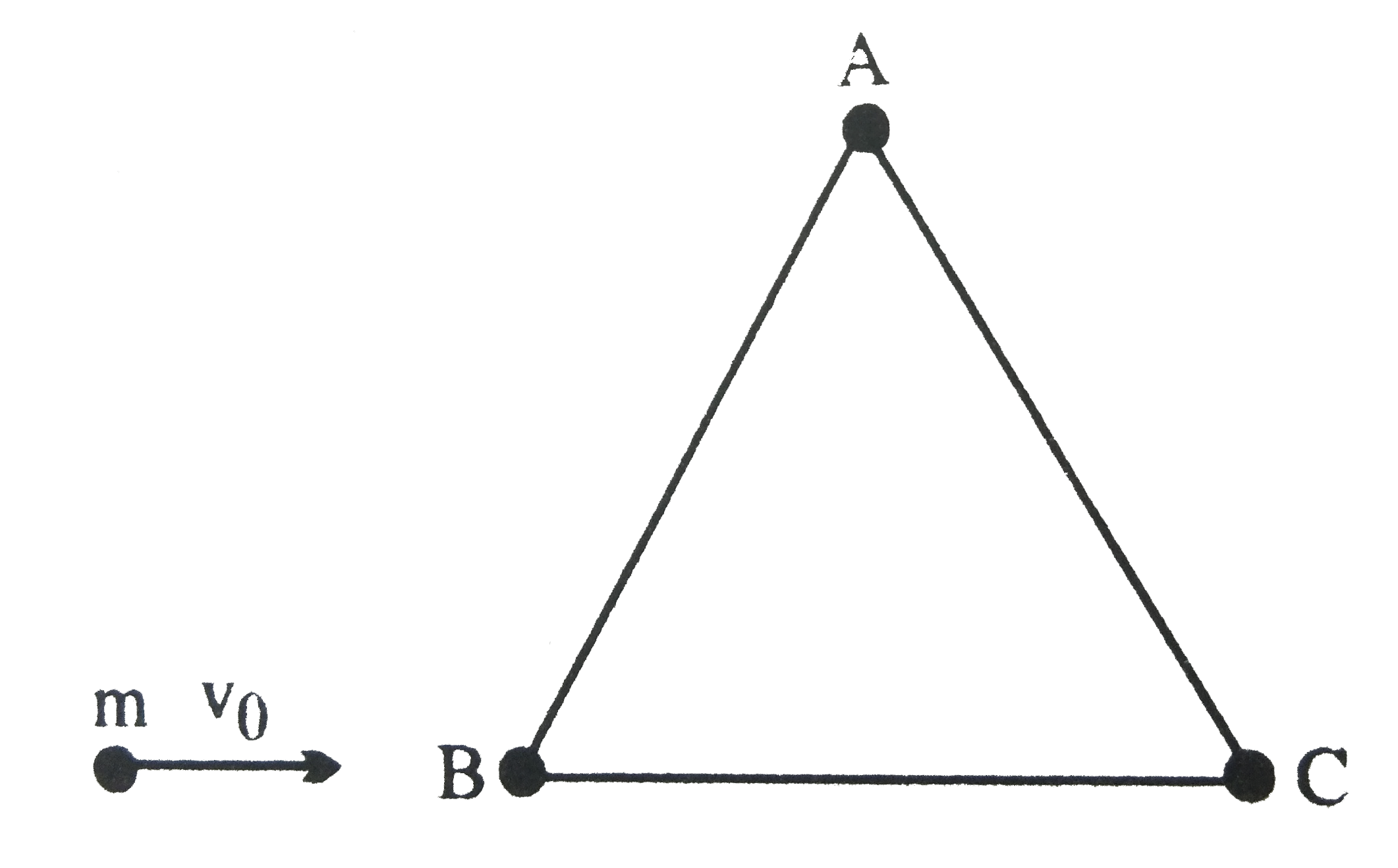
(i) Calculate the time required by the triangle ABC to complete half-revolution in its subsequent motion.
(ii) What is the net displacement of point B during this interval ?
View SolutionThree particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View Solution
Knowledge Check
Three particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
A−3Gm22bB−Gm22bC−3Gm2bD−Gm2bThree particles each of mass 2kg are at the corners of an equilateral triangle of side √3m. If one of the particles is removed, the shift in the centre of mass is
A0.2mB0.5mC0.4mD0.3mThree particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
At=dvBt=3d2vCt=2d3vDt=0
Three particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View SolutionThree identical particles each of mass m are placed at the vertices of an equilateral triangle of side a. Fing the force exerted by this system on a particle P of mass m placed at the
(a) the mid point of a side
(b) centre of the triangle
View SolutionThree identical particles each of mass m are placed at the vertices of an equilateral triangle of side a. Fing the force exerted by this system on a particle P of mass m placed at the

(a) the mid point of a side
(b) centre of the triangle
View SolutionThree particles A,B and C each of mass m are lying at the corners of an equilateral triangle of side L . If the particle A is released keeping the particles B and C fixed , the magnitude of instantaneous acceleration of A is
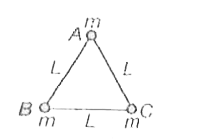
View SolutionThree particles A,B and C each of mass m are lying at the corners of an equilateral triangle of side L . If the particle A is released keeping the particles B and C fixed , the magnitude of instantaneous acceleration of A is

View Solution
