In each situation of Column - I a uniform disc of mass m and radius R rolls on a rough fixed horizontal surface a shown. At (initially) the angular velocity of the disc is and velocity of the centre of mass of the disc is (in horizontal direction). The relation between and is given for each situation and also initial sense of rotation is given for each situation in column I Then match the statments in Column I with the corresponding results in Column II.

The correct Answer is:A-P,Q,R;B-P,R;C-P,Q;D-P,QR
Topper's Solved these Questions
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - IV) (LEVEL - II Integer Type Questions)
6 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - V) (LEVEL - II More than One correct answer Type Questions)
7 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - IV) (LEVEL - II Linked Comprehension Type Questions)
5 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
Similar Questions
In each situation of column -I a uniform disc of mass m and radius R rolls on a rough fixed horizontal surface as shown At t=0 (initially)the angular velocity of disc is omega_(0) and velocity of centre of mass of disc is v_(0) (in horizontal direction). The relation between v_(0) and ω0 and the initial sense of rotation is given for each situation in column-I then match the statement in column-I with the corresponding results in column-II.
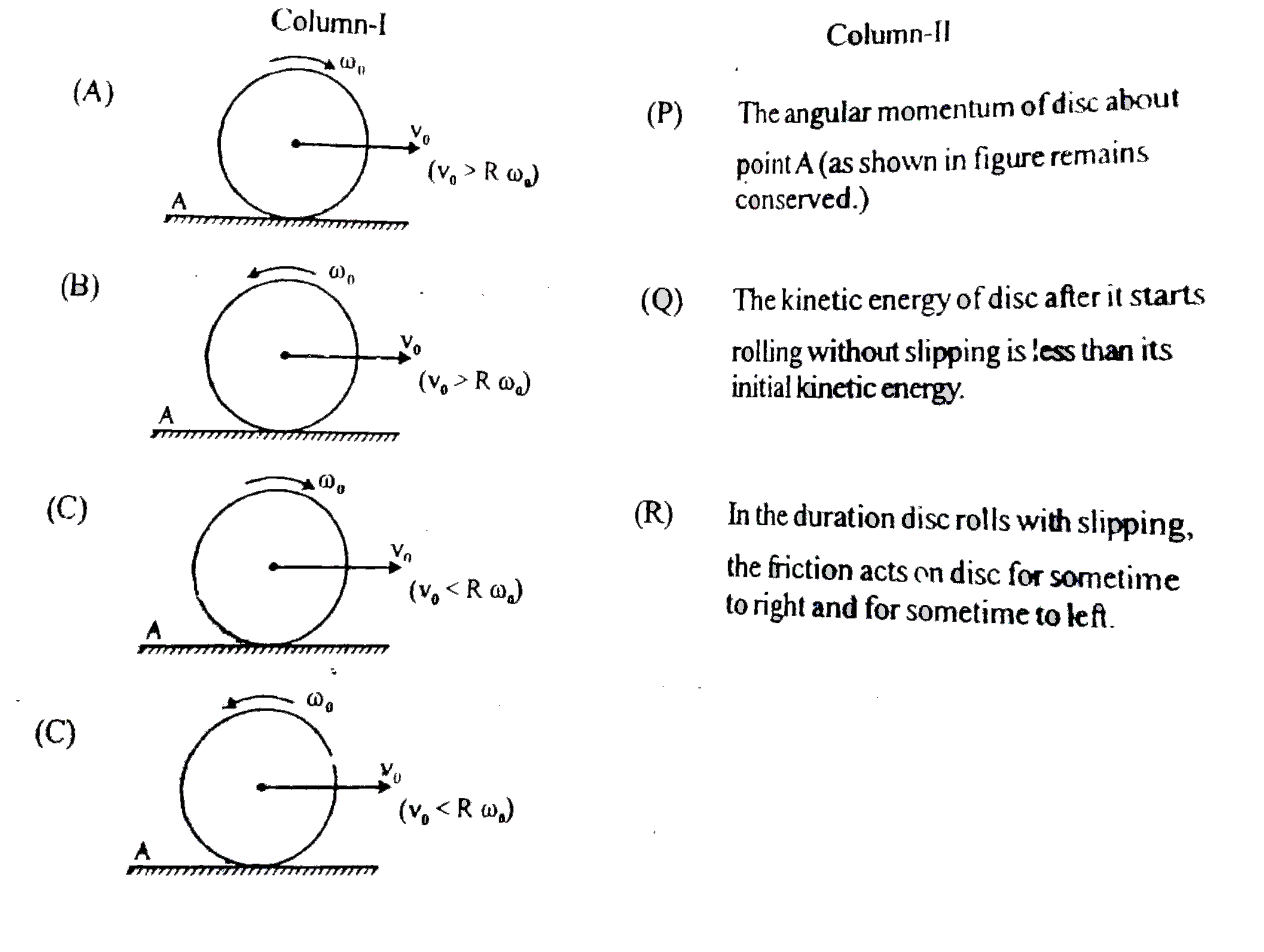
View SolutionIn each situation of Table-1, a uniform disc of mass m and radius R rolls on a rough fixed horizontal surface as shown. At, t=0 (initially) the angular velocity of disc is ω0 and velocity of centre of mass of disc is v0 (in horizontal direction). The relation between v0 and ω0 for each situation and also initial sense of rotation is given in Table-1 . Then match the statements in Table-1 with the corresponding results in Table-2.

View Solution
Knowledge Check
A point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts
 A(2u3R)B(3u3R)C(5u3R)D(2u5R)
A(2u3R)B(3u3R)C(5u3R)D(2u5R)A disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:
 A3v22gB4v24gCv24gDv22g
A3v22gB4v24gCv24gDv22gA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:
 A3v22gB3v24gCv24gDv22g
A3v22gB3v24gCv24gDv22g
In each situation of Table-1, a uniform disc of mass m and radius R rolls on a rough fixed horizontal surface as shown. At, t=0 (initially) the angular velocity of disc is ω0 and velocity of centre of mass of disc is v0 (in horizontal direction). The relation between v0 and ω0 for each situation and also initial sense of rotation is given in Table-1 . Then match the statements in Table-1 with the corresponding results in Table-2.

View SolutionA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts

View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be :-
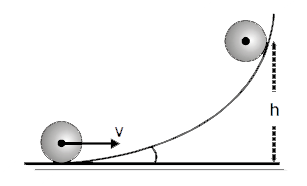
View Solution
