A semicircular ring of mass m and radius r is relesed from rest in the position shown with its lower edge resting on a horizontal surface. Minimum coefficient of static friction μs which is necessary to prevent any initial slipping of the ring is x/10, value of x is
2
3
4
5
The correct Answer is:C
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LEVEL - II LECTURE SHEET (ADVANCED) More than One correct answer Type Questions14videos
ROTATIONAL DYNAMICS
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - LEVEL - II LECTURE SHEET (ADVANCED) Linked comprehension Type Questions6videos
ROTATIONAL DYNAMICS
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (Exercise - VI) (LEVEL - II Matrix Matching Type Questions)3videos
ROTATIONAL DYNAMICS
- BOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)6videos
RIVISION EXERCISE
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers20videos
ROTATIONAL MECHANICS
Similar Questions
The uniform cubical slab of side 'a' is released from rest in the position shown in the figure. For what value of 'x' is the angular acceleration maximum ( friction between the surface and cube is sufficient to prevent any slipping ?
View SolutionA force (F=Mg) is applied on the top of a circular ring of mass M and radius R kept on a rough horizontal surface. If the ring rolls without slipping, then minimum coefficient of friction required is
_PHY_E05_236_Q01.png)
View Solution
Knowledge Check
- Question 1 - Select One
The uniform cubical slab of side 'a' is released from rest in the position shown in the figure. For what value of 'x' is the angular acceleration maximum ( friction between the surface and cube is sufficient to prevent any slipping ?
A√56aB√58aC√510aD√512a - Question 2 - Select One
A ring of mass M and radius R is released on an inclined as shown. If the coefficient of friction μ<12tanθ, then during a displacement l:
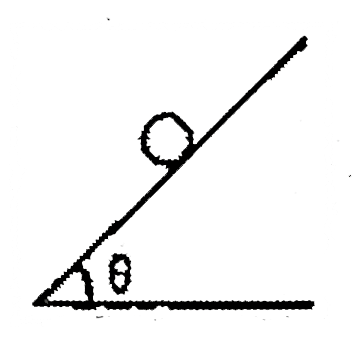AAcceleration of the ring =g/2sinθBAcceleration of the ring =gsinθ−μgcosθCwork done by the force of friction =mgl(sinθ−ucosθ)Dwork done by the force of friction is zero - Question 3 - Select One
A blocky of mass m rests on a horizotal floor with which it has a coefficient of static friction μ. It is desired to make the body move by applying the minimum possible force F. Find the magnitude of F and the direction in which it has be applies.
AμmgB√1+μ2μmgCμ√1+μ2mgDμmg√1+μ2
A force (F = Mg) is applied on the top of a circular ring ofmass M and radius R keot on a rough horizontal surface. If the ring rolls without slipping, the minimum coefficient of friction required is
_PHY_214_Q01.png)
View SolutionFor identical rods, each of mass m are welded at their ends to form a square, and the corners are then welded to a light metal hoop of radius r. If the rigid assembly of rods and hoop is allowed to roll down the inclined rough surface. If the minimum value of the coefficient of static friction which will prevent slipping is k10 . Find the value of k.
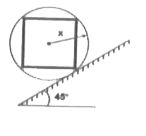
View SolutionFor identical rods, each of mass m are welded at their ends to form a square, and the corners are then welded to a light metal hoop of radius r. If the rigid assembly of rods and hoop is allowed to roll down the inclined rough surface. If the minimum value of the coefficient of static friction which will prevent slipping is k10 . Find the value of k.
View SolutionA mass m rests under the action of a force F as shown in the figure-2.158 on a horizontal surface. The coefficient of friction between the mass and the surface is μ. The force of friction between the mass and the surface is :
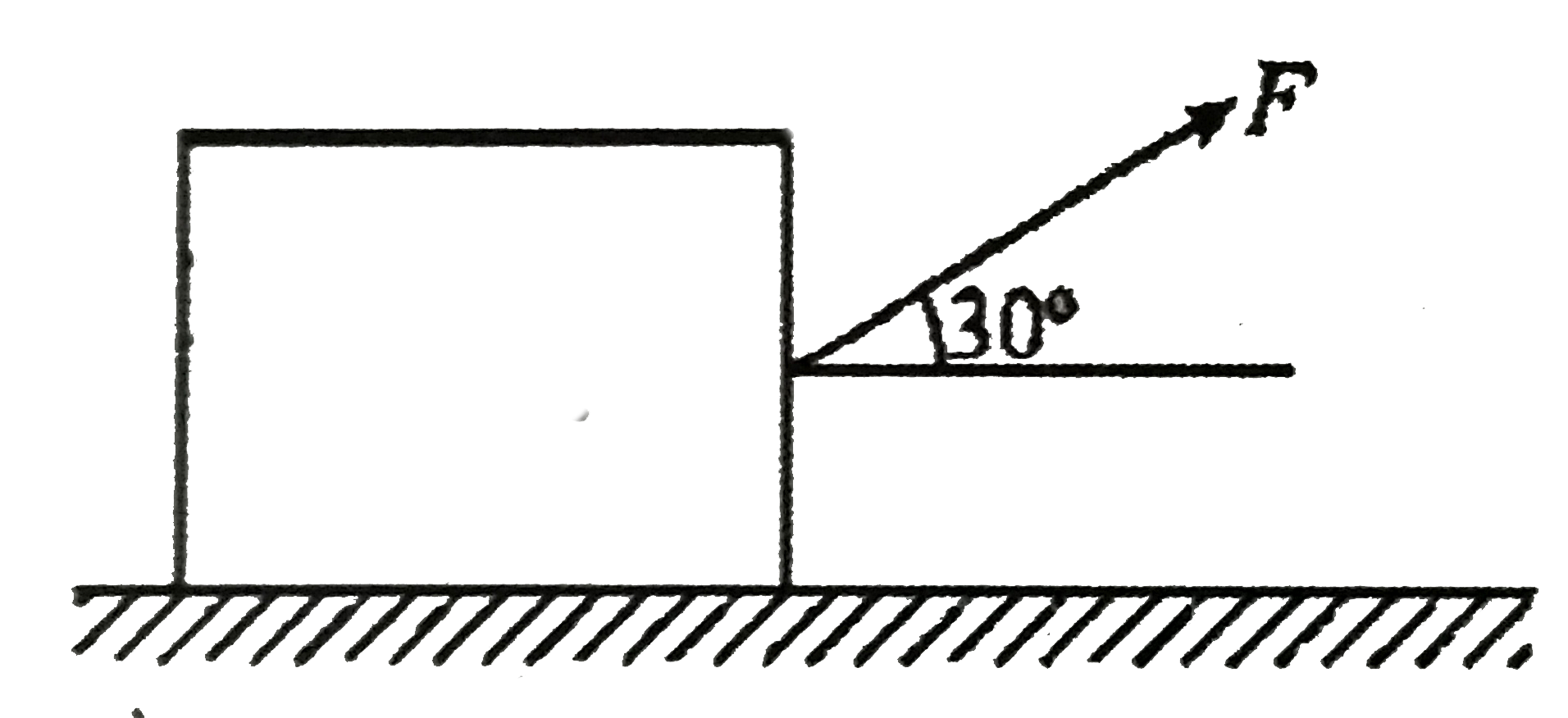
View SolutionA uniform circular ring of radius R is first rotated about its horizontal axis with an angular velocity ω0 and then carefully placed on a rough horizontal surface as shown. The coefficient of friction between the surface and the rings μ. Time after which its angular speed is reduced to 0.5ω0 is
View Solution