Let t1=(sin−1x)sin−1x,t2=(sin−1x)cos−1x,t3=(cos−1x)sin−1x,t4=(cos−1x)cos−1x
Match the items of Column I with the items Column II
Column-IColumn-IIA) x∈(0,cos1)p) t1>t2>t4>t3B) x∈(cos1,1√2)q) t4>t3>t1>t2C) x∈(1√2,sin1)r) t1>t2>t4>t3D) x∈(sin1,1)s) t3>t4>t1>t2
Text Solution
The correct Answer is:A-q, B-s, C-r, D-p
|
Topper's Solved these Questions
- INVERSE TRIGNOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSE TRIGNOMETRIC FUNCTIONSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II PRACTICE SHEET (ADVANCED) STATEMENT TYPE QUESTIONS)
4 Videos
- INVERSE TRIGNOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSE TRIGNOMETRIC FUNCTIONSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
7 Videos
- INVERSE TRIGNOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSE TRIGNOMETRIC FUNCTIONSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II PRACTICE SHEET (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
3 Videos
- HYPERBOLIC FUNCTIONS BOOK - AAKASH SERIESCHAPTER - HYPERBOLIC FUNCTIONS EXERCISE - PRACTICE SHEET EXERCISE-II (STRAIGHT OBJECTIVE TYPE QUESTIONS)
18 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - AAKASH SERIESCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - PRACTICE EXERCISE
37 Videos
Similar Questions
Knowledge Check
Let t1=(sin−1x)sin−1x,t2=(sin−1x)cos−1x,t3=(cos−1x)sin−1xandt4=(cos−1x)cos−1x Match the column I with column II and mark the correct option from the given codes.
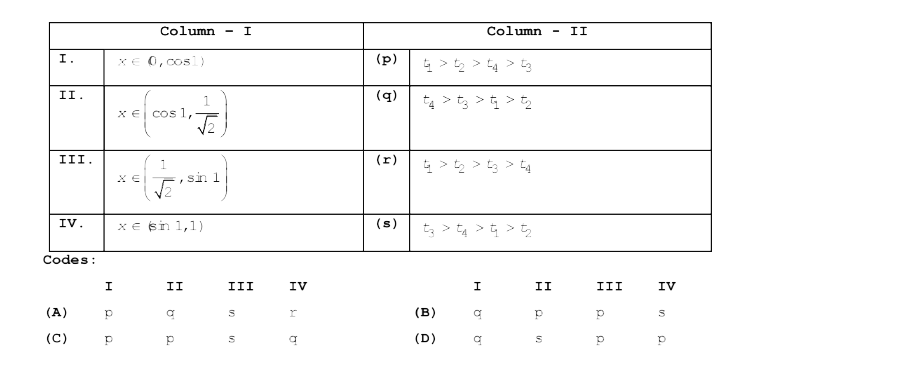 AIIIIIIIVpqsrBIIIIIIIVqppsCIIIIIIIVppsqDIIIIIIIVqspp
AIIIIIIIVpqsrBIIIIIIIVqppsCIIIIIIIVppsqDIIIIIIIVqsppIf x=sin−1(t2−1),y=cos−1(2t) then dydx at t = 0 is
A−√2B−1√2C√2D1√2f(x)=∫x0et3(t2−1)(t+1)2011dt(x>0) then :
AThe number of point iof inflections is atleast 1BThe number of point of inflectins is 0CThe number of point of local maxima is 1DThe number of point of local minima is 1
Examine the following plots and predict whether in (i) P1<P2andT1>T2 , in (ii) T1=T2<T3, in (iii) V1>V2,in(iv)P1>P2orP2>P1
_E01_267_Q01.png)
View Solutionf(x)=∫x0et3(t2−1)(t+1)2011dt(x>0) then :
View SolutionIf Tn=sinnx+cosnx, prove that 2T6−3T4+1=0
View SolutionFor 1 mol of an ideal gas, V1>V2>V3 in fig. 1, T1>T2>T3 in fig. 2, P1>P2>P3 in fig. 3, and T1>T2>T3 in fig. 4, then which curves are correct.
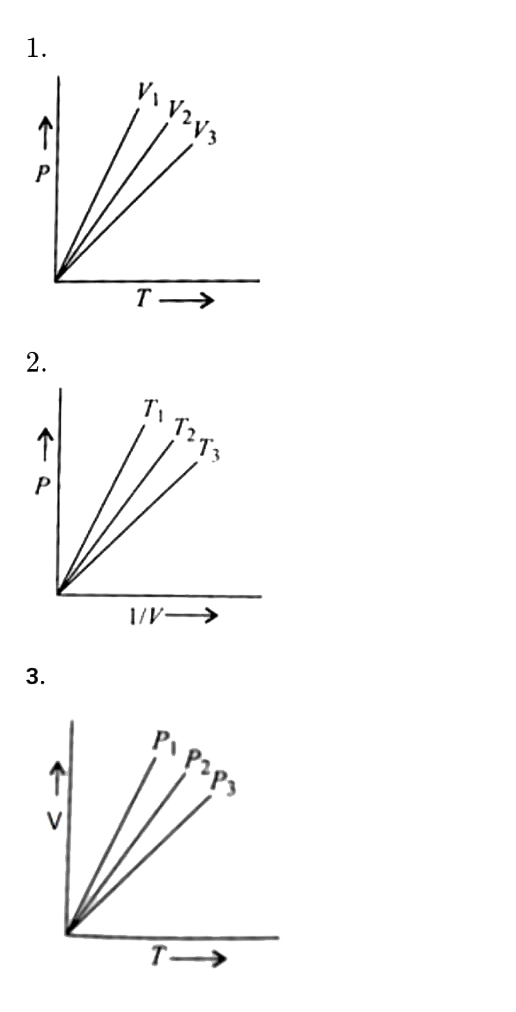
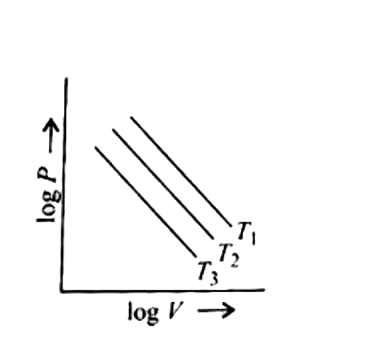
View SolutionIf x=sin−1(3t−4t8) and y=cos−1(√1−t2), then dy/dx is equal to
View Solution

