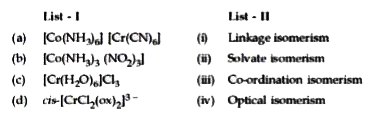Match List-I with List-II : List-I:
List-IList-II(a)h(Plank's constant)(i)[MLT−1](b)E(Kinetic energy)(ii)[ML2T−1](c)V(elecic potential)(iii)[ML2T−2](d)P(linear momentum)(iv)[ML2I−1T−3]
Choose the correct answer from the options given below :
(a)→(iii),(b)→(iv),(c)→(ii),(d)→(i)
(a)→(ii),(b)→(iii),(c)→(iv),(d)→(i)
(a)→(i),(b)→(ii),(c)→(iv),(d)→(iii)
(a)→(iii),(b)→(ii),(c)→(iv),(d)→(iii)
The correct Answer is:B
To solve the problem of matching List-I with List-II based on the dimensional formulas, we will analyze each item in List-I and determine its dimensional formula. Then, we will match it with the corresponding item in List-II.
Step 1: Determine the Dimensional Formula of Planck's Constant (h)
Planck's constant (h) relates energy (E) and frequency (ν) through the equation:
E=hν
We can also express momentum (p) in terms of Planck's constant:
p=hλ
Where λ is the wavelength.
From the momentum formula:
h=p⋅λ
The dimensional formula for momentum (p) is:
(p)=(M)(L)(T−1)
And the dimensional formula for wavelength (λ) is:
(λ)=(L)
Thus, we have:
(h)=(p)⋅(λ)=(M)(L)(T−1)⋅(L)=(M)(L2)(T−1)
So, the dimensional formula for Planck's constant is:
(h)=(M)(L2)(T−1)
Step 2: Determine the Dimensional Formula of Kinetic Energy (E)
The formula for kinetic energy (E) is:
E=12mv2
Where m is mass and v is velocity.
The dimensional formula for mass (m) is:
(m)=(M)
And the dimensional formula for velocity (v) is:
(v)=(L)(T)
Thus, the dimensional formula for kinetic energy is:
(E)=(M)⋅((L)(T))2=(M)(L2)(T−2)
Step 3: Determine the Dimensional Formula of Electric Potential (V)
The formula for electric potential (V) is given by:
V=WQ
Where W is work done and Q is charge.
Work done (W) can be expressed as:
W=F⋅d
Where F is force and d is displacement.
The dimensional formula for force (F) is:
(F)=(M)(L)(T−2)
And for displacement (d):
(d)=(L)
Thus, the dimensional formula for work done is:
(W)=(F)(d)=(M)(L)(T−2)⋅(L)=(M)(L2)(T−2)
Now, the dimensional formula for charge (Q) is:
(Q)=(I)(T)
Where I is current.
Thus, the dimensional formula for electric potential is:
(V)=(W)(Q)=(M)(L2)(T−2)(I)(T)=(M)(L2)(T−3)(I−1)
Step 4: Determine the Dimensional Formula of Linear Momentum (P)
The formula for linear momentum (P) is:
P=mv
Where m is mass and v is velocity.
Thus, the dimensional formula for linear momentum is:
(P)=(M)⋅((L)(T))=(M)(L)(T−1)
Step 5: Match List-I with List-II
Now we can match the dimensional formulas obtained with those in List-II:
- (a) Planck's constant (h): (M)(L2)(T−1) → Matches with (ii) (M)(L2)(T−1)
- (b) Kinetic energy (E): (M)(L2)(T−2) → Matches with (iii) (M)(L2)(T−2)
- (c) Electric potential (V): (M)(L2)(T−3)(I−1) → Matches with (iv) (M)(L2)(I−1)(T−3)
- (d) Linear momentum (P): (M)(L)(T−1) → Matches with (i) (M)(L)(T−1)
Final Matching:
- (a) → (ii)
- (b) → (iii)
- (c) → (iv)
- (d) → (i)
Conclusion:
The correct answer is option 2.
E=hν
We can also express momentum (p) in terms of Planck's constant:
p=hλ
Where λ is the wavelength.
h=p⋅λ
The dimensional formula for momentum (p) is:
(p)=(M)(L)(T−1)
And the dimensional formula for wavelength (λ) is:
(λ)=(L)
(h)=(p)⋅(λ)=(M)(L)(T−1)⋅(L)=(M)(L2)(T−1)
So, the dimensional formula for Planck's constant is:
(h)=(M)(L2)(T−1)
E=12mv2
Where m is mass and v is velocity.
(m)=(M)
And the dimensional formula for velocity (v) is:
(v)=(L)(T)
(E)=(M)⋅((L)(T))2=(M)(L2)(T−2)
V=WQ
Where W is work done and Q is charge.
W=F⋅d
Where F is force and d is displacement.
(F)=(M)(L)(T−2)
And for displacement (d):
(d)=(L)
(W)=(F)(d)=(M)(L)(T−2)⋅(L)=(M)(L2)(T−2)
(Q)=(I)(T)
Where I is current.
(V)=(W)(Q)=(M)(L2)(T−2)(I)(T)=(M)(L2)(T−3)(I−1)
P=mv
Where m is mass and v is velocity.
(P)=(M)⋅((L)(T))=(M)(L)(T−1)
- (b) Kinetic energy (E): (M)(L2)(T−2) → Matches with (iii) (M)(L2)(T−2)
- (c) Electric potential (V): (M)(L2)(T−3)(I−1) → Matches with (iv) (M)(L2)(I−1)(T−3)
- (d) Linear momentum (P): (M)(L)(T−1) → Matches with (i) (M)(L)(T−1)
- (a) → (ii)
- (b) → (iii)
- (c) → (iv)
- (d) → (i)
The correct answer is option 2.
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS (SECTION-B)
10 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - (SECTION - A)
20 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Knowledge Check
Match List-I with List-II.

Choose the correct answer from the options given below :A(a)-(iv), (b)-(iii), (c)-(ii), (d)-(i)B(a)-(ii), (b)-(iv), (c)-(i), (d)-(iii)C(a)-(i), (b)-(ii), (c)-(iii), (d)-(iv)D(a)-(iii), (b)-(i), (c)-(iv), (d)-(ii)Match List I with List II.
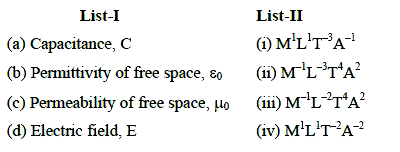
Choose the correct answer from the options given belowA(a) → (iii), (b) → (ii), (c ) → (iv), (d) → (i)B(a) → (iii), (b) → (iv), (c ) → (ii), (d) → (i)C(a) → (iv), (b) → (ii), (c ) → (iii), (d) → (i)D(a) → (iv), (b) → (iii), (c ) → (ii), (d) → (i)Match List-I and List - II .
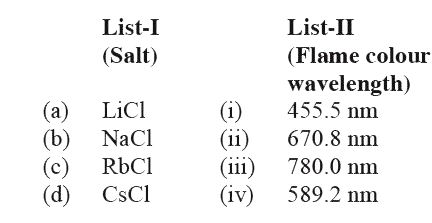
Choose the correct answer from the options given below :A(a)-(iv), (b)-(ii), (c)-(iii), (d)-(i)B(a)-(ii), (b)-(i), (c)-(iv), (d)-(iii)C(a)-(i), (b)-(iv), (c)-(ii), (d)-(iii)D(a)-(ii), (b)-(iv), (c)-(iii), (d)-(i)
Match List-I with List-II

Choose the correct answer from the options given below:
View SolutionMatch List-I with List-II
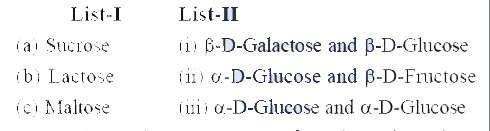
Choose the correct answer from the options given below :
View SolutionMatch List-I with List-II

Choose the correct answer from the options given below:
View SolutionMatch List-I with List-II
Choose the correct answer from the options given below:
View SolutionMatch List I with List II :

Choose the correct answer from the options given below :
View Solution