A small bob tied at one end of a thin string of length 1m is describing a vertical circle so that the maximum and minimum tension in the string are in the ratio 5: 1. The velocity of the bob at the height position is ____ m/s. (Take g=10m/s2)
The correct Answer is:5
To solve the problem, we need to find the velocity of the bob at the highest point of its vertical circular motion, given that the maximum and minimum tensions in the string are in the ratio of 5:1.
1. Identify the Forces at the Highest and Lowest Points:
- At the highest point (Point B), the forces acting on the bob are its weight (mg) acting downwards and the tension (T_min) in the string also acting downwards.
- At the lowest point (Point A), the forces are the weight (mg) acting downwards and the tension (T_max) acting upwards.
2. Write the Equations for Tension:
- At the highest point (B):
Tmin+mg=mv22r
Rearranging gives:
Tmin=mv22r−mg(Equation 1)
- At the lowest point (A):
Tmax−mg=mv21r
Rearranging gives:
Tmax=mv21r+mg(Equation 2)
3. Use the Ratio of Tensions:
- Given that Tmax:Tmin=5:1, we can write:
Tmax=5Tmin
- Substitute the expressions from Equations 1 and 2 into this ratio:
mv21r+mgmv22r−mg=5
4. Cross Multiply and Simplify:
- Cross multiplying gives:
mv21r+mg=5(mv22r−mg)
- Expanding and rearranging:
mv21r+mg=5mv22r−5mg
mv21r+6mg=5mv22r
5. Solve for v1:
- Rearranging gives:
mv21+6mgr=5mv22
- Dividing through by m:
v21+6gr=5v22
6. Use Conservation of Energy:
- The total mechanical energy at the lowest point (A) and the highest point (B) must be equal:
12mv21=12mv22+mg(2r)
- Simplifying gives:
v21=v22+4gr
7. Substitute v1^2 into the Tension Equation:
- Substitute v21 from the energy equation into the tension equation:
(v22+4gr)+6gr=5v22
- This simplifies to:
10gr=4v22
- Rearranging gives:
v22=10gr4=5gr2
8. Substitute g and r:
- Given g=10m/s2 and r=1m:
v22=5×10×12=25
- Therefore, v2=√25=5m/s.
Final Answer:
The velocity of the bob at the highest position is 5 m/s.
- At the highest point (Point B), the forces acting on the bob are its weight (mg) acting downwards and the tension (T_min) in the string also acting downwards.
- At the lowest point (Point A), the forces are the weight (mg) acting downwards and the tension (T_max) acting upwards.
- At the highest point (B):
Tmin+mg=mv22r
Rearranging gives:
Tmin=mv22r−mg(Equation 1)
- At the lowest point (A):
Tmax−mg=mv21r
Rearranging gives:
Tmax=mv21r+mg(Equation 2)
- Given that Tmax:Tmin=5:1, we can write:
Tmax=5Tmin
- Substitute the expressions from Equations 1 and 2 into this ratio:
mv21r+mgmv22r−mg=5
- Cross multiplying gives:
mv21r+mg=5(mv22r−mg)
- Expanding and rearranging:
mv21r+mg=5mv22r−5mg
mv21r+6mg=5mv22r
- Rearranging gives:
mv21+6mgr=5mv22
- Dividing through by m:
v21+6gr=5v22
- The total mechanical energy at the lowest point (A) and the highest point (B) must be equal:
12mv21=12mv22+mg(2r)
- Simplifying gives:
v21=v22+4gr
- Substitute v21 from the energy equation into the tension equation:
(v22+4gr)+6gr=5v22
- This simplifies to:
10gr=4v22
- Rearranging gives:
v22=10gr4=5gr2
- Given g=10m/s2 and r=1m:
v22=5×10×12=25
- Therefore, v2=√25=5m/s.
The velocity of the bob at the highest position is 5 m/s.
Topper's Solved these Questions
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:(SECTION - A)
Explore 20 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:(SECTION - B)
Explore 10 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:PHYSICS (SECTION-A)
Explore 20 Videos
- JEE MAINBook:JEE MAINS PREVIOUS YEARChapter:JEE MAINExercise:All Questions
Explore 473 Videos
- JEE MAIN 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2022Exercise:Question
Explore 492 Videos
Similar Questions
A small sphere tied to the string of length 0.8m is describing a vertical circle so that the maximum and minimum tensions in the string are in the ratio 3:1. The fixed end of the string is at a height of 5.8m above ground.
(a) Find the velocity of the sphere at the lowest position.
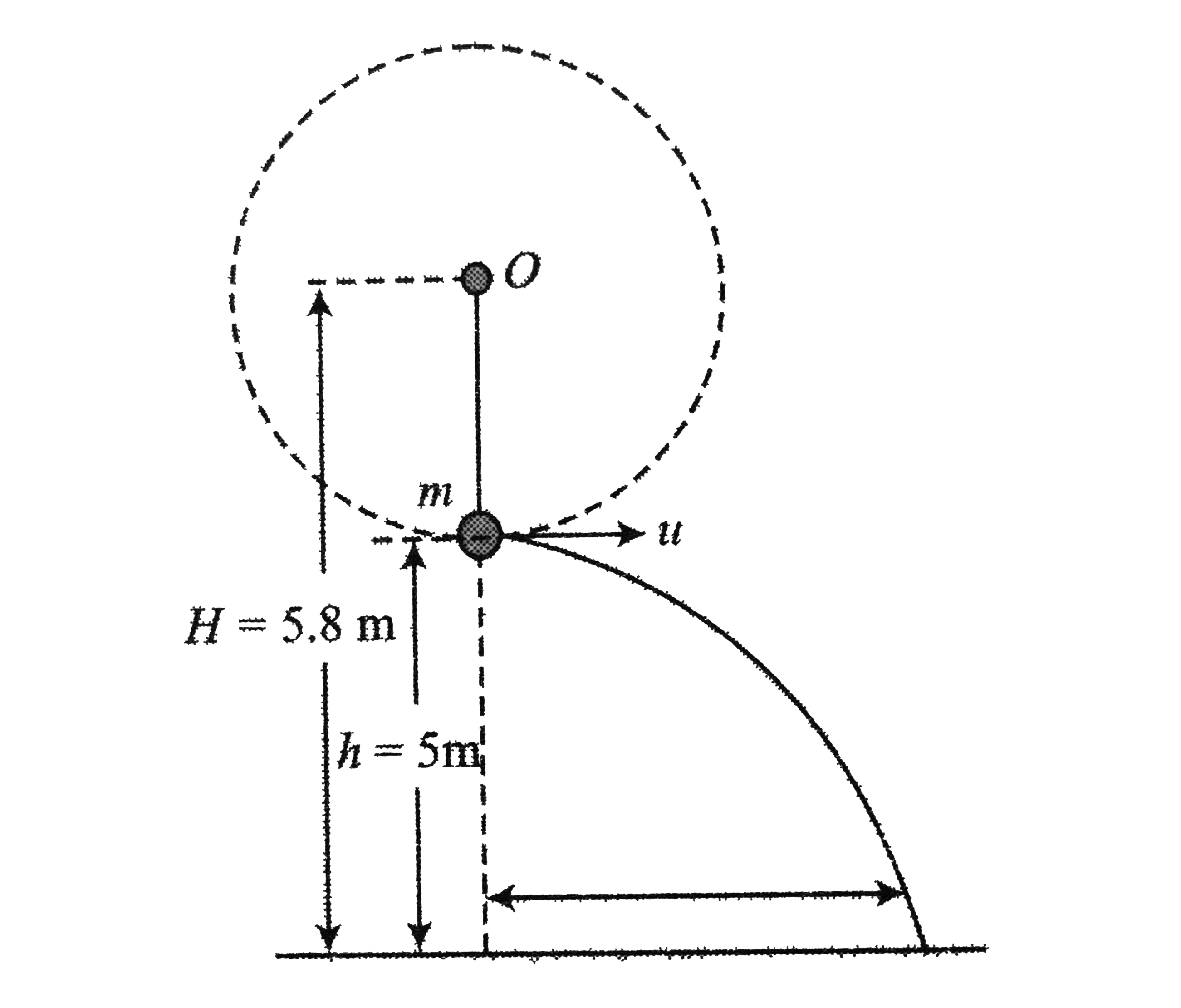
(b) If the string suddenly breaks at the lowest position, when and where will the sphere hit the ground?
View SolutionA small sphere tied to the string of length 0.8m is describing a vertical circle so that the maximum and minimum tensions in the string are in the ratio 3:1. The fixed end of the string is at a height of 5.8m above ground.
(a) Find the velocity of the sphere at the lowest position.

(b) If the string suddenly breaks at the lowest position, when and where will the sphere hit the ground?
View Solution
Knowledge Check
For a particle rotating in a vertical circle with uniform speed, the maximum and minimum tension in the string are in the ratio 5 : 3. If the radius of vertical circle is 2 m, the speed of revolving body is (g=10m/s2)
A√5m/sB4√5m/sC5 m/sD10 m/sA stone of mass 1 kg tied to a light inextensible string of length L=53m, is whirling in a vertical circle of radius L. If the ratio of the maximum and minimum tension in the string is 4 and g=10m/s2, the speed of stone at the highest point of the circle is
A5m/sB5√3m/sC5√2m/sD10m/sA stone of 1 kg tied up with 10/3 m long string rotated in a vertical circle. If the ratio of maximum and minimum tension in string is 4 then speed of stone at highest point of circular path will be ( g=10ms2)
A20m/sB10√3m/sC5√2m/sD10m/s
A body of mass 100 gram is tied at the end of a string of length 1m. It is rotated in a vertical circle at a critical speed of 4 m/s at the highest point . The tension in the string at the huighest point in its path is [ take g=10m/s2]
View SolutionThe maximum and minimum tension in the string whirling in a circle of radius 2.5 m with constant velocity are in the ratio 5:3 then its velocity is
View SolutionA body of mass 100 gram , tied at the end of a string of length 3m rotes in a vertical circle and is just able to complete the circle . If the tension in the string at its lowest point is 3.7 N, then its angular velocity will be _____
[g=10m/s2]
View SolutionA small pot completely filled with water is tied at the end of a 1.6 m long string . It is whirled in a vertical circle what minimum speed should be given to the pot , so that the water from the pot does not spill when the pot is at the highest postion ? ( use g=10m/s2)
View SolutionA point mass of 2 kg tied to a string of 1 m length is rotated in a vertical circle with uniform speed of 4m/s. The tension in the string is nearly 32 N when mass is at
View Solution
