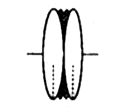
Two identical equiconvex lenses, each of focal length f, are placed side by side in contact with each other with a layer of water in between them as shown in the figure. If refractive index of the material of the lenses is greater than that of water, how the combined focal length F is related to f?
 Solution in Bengali
Solution in Bengali
F>f
f2<F<f
F<f2
F=f
Step by step video & image solution for Two identical equiconvex lenses, each of focal length f, are placed side by side in contact with each other with a layer of water in between them as shown in the figure. If refractive index of the material of the lenses is greater than that of water, how the combined focal length F is related to f? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Radon-222 has a half- life of 3.8 days. If one starts with 0.064 kg of Radon-222. the quantitiy of Radon-222 left after 19 days will be
View SolutionA projectile thrown with an initial velocity of 10ms−1 at an angle a with the horizontal, has a range of 5 m . Taking g=10ms−2 and neglecting air resistance, what will be the estimated value of α ?
View SolutionTwo identical glass (μg=3/2) equiconvex lenses of focal length f are kept ini contact. The space between the two lenses is filled with water (μw=4/3). The focal length of the combination is
View SolutionTwo identical glass (mu_(g)=3//2) equiconvex lenses of focal length f are kept ini contact. The space between the two lenses is filled with water (mu_(w)=4//3) . The focal length of the combination is
View SolutionTwo equi-convex lenses, each of radius of curvature 20 cm and refractive index 1.5 are placed in contact. If water of refractive index 4/3 is placed in between the lenses, the focal length of the combination is,
View SolutionTwo equi-convex lenses, each of radius of curvature 20 cm and refractive index 1.5 are placed in contact. If water of refractive index 43is placed in between the lenses, the focal length of the combination is,
View SolutionTwo identical equiconvex lenses of refractive index 3/2 and focal length 16 cm are kept in contact. The space between the lenses is filled with water of refractive index 4/3. What is the focal length of the combination ?
View SolutionTwo identical glass (mu_g=3/2) equiconvex lenses of focal length f each are kept in contact. The space between the two lenses is filled with water mu_w=4/3 . The focal length of the combination is
View SolutionTwo identical glass (mu_(g)=3//2) equiconvex lenses of focal length f are kept in contact. The space between the two lenses is filled with water (mu_(w)=4//3) . The focal length of the combination is
View SolutionTwo identical glass equiconvex lenses of focal length f each are kept in contact. The space between the two lenses is filled with water . The focal length of the combination is
View SolutionTwo identical glass (mu_(g)=3//2) equiconvex lenses of focal length f are kept in contact. The space between the two lenses is filled with water (mu_(w)=4//3) . The focal length of the combination is
View SolutionTwo similar thin equiconvex lenses, of focal length f each, are kept coaxially in contact with each other such that the focal length of the combination is F_1 . When the space between the two lenses is filled with glycerin (which has the same refractive index (mu = 1.5) as that of glass) then the equivalent focal length is f_2 . The ratio F_1 : F_2 will be:
View SolutionTwo identical equiconvex lenses, each of focal length 'f' are placed side by side in contact with each other with a layer of water in between them as shown in the figure. If refractive index of the material of the lenses is greater than that of water, how the combined focal length 'F' is related of 'f'?
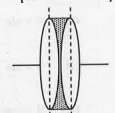
View SolutionTwo identical glass (μg=3/2) equiconvex lenses of focal length f are kept ini contact. The space between the two lenses is filled with water (μw=4/3). The focal length of the combination is
View SolutionWhen two thin converging lenses of focal lengths f, and f, are held in contact with each other, calculate the power of the combination.
View Solution
