A river of width 'w' is flowing variable velocity given by vr=v0(1+√3−1wy). Where 'y' is perpendicular distance from one bank. A boat is driven such that it moves perpendicular to bank. Velocity of boat in still water is 2V(0)
Time taken to reach other bank
πw6(√3−1)V0
w6√3−1V0)
w6(√3+1)V0
πw3(√3−1)V0
The correct Answer is:A
Topper's Solved these Questions
- KINEMATICSBOOK - AAKASH SERIESCHAPTER - KINEMATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED)) (Matrix Matching Type Questions)
1 Videos
- KINEMATICSBOOK - AAKASH SERIESCHAPTER - KINEMATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED)) (Integer Type Questions)
12 Videos
- KINEMATICSBOOK - AAKASH SERIESCHAPTER - KINEMATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED)) (More than One correct answer Type Questions)
3 Videos
- HORIZONTAL CIRCULAR MOTIONBOOK - AAKASH SERIESCHAPTER - HORIZONTAL CIRCULAR MOTIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) Integer Type Questions)
3 Videos
- KINETIC THEORY OF GASESBOOK - AAKASH SERIESCHAPTER - KINETIC THEORY OF GASESEXERCISE - Practice Exercise
15 Videos
Similar Questions
The width of a river is 2√3 km. A boat is rowed in direction perpendicular to the banks of river. If the drift of the boat due to flow is 2 km, the displacement of the boat is
View SolutionThe current velocity of river grows in proportion to the distance from its bank and reaches the maximum value v0 in the middle. Near the banks the velocity is zero. A boat is moving along the river in such a manner that the boatman rows his boat always perpendicular to the current. The speed of the boat in still water is u. Find the distance through which the boat crossing the river will be carried away by the current, if the width of the river is c. Also determine the trajectory of the boat.
View Solution
Knowledge Check
A river of width w is flowing such that the stream velocity varies with y as vR=v0[1+√3−1wy], where y is the perpendicular distance from one bank.A boat starts rowing from the bank with constant velocity v=2v0 in such a way that it always moves along a straight line perpendicular to the banks.
What will be the velocity of the boat along the straight line when he reaches the other bankAv0B√2v0Cv0√2D2c0A river of width w is flowing such that the stream velocity varies with y as vR=v0[1+√3−1wy], where y is the perpendicular distance from one bank.A boat starts rowing from the bank with constant velocity v=2v0 in such a way that it always moves along a straight line perpendicular to the banks.
At what time will he reach the other bankAt=wπ6v0Bwπ6(√2−1)v0Cwπ6(√3−1)v0Dwπ(√3−1)v0The width of a river is 2√3km.A boat is rowed in direction perpendicular to the banks of river.If the drift of the boat due to flow is 2km,the displacement of the boat is.
A3kmB6kmC5kmD4km
The current velocity of river grows in proportion to the distance from its bank and reaches the maximum value v0 in the middle. Near the banks the velocity is zero. A boat is moving along the river in such a manner that the boatman rows his boat always perpendicular to the current. The speed of the boat in still water is u. Find the distance through which the boat crossing the river will be carried away by the current, if the width of the river is c. Also determine the trajectory of the boat.
View SolutionA river is flowing with velocity 5km/hr as shown in the figure. A boat start from A and reaches the other bank by covering shortest possible distance. Velocity of boat in still water is 3km/hr. The distance boat covers is.

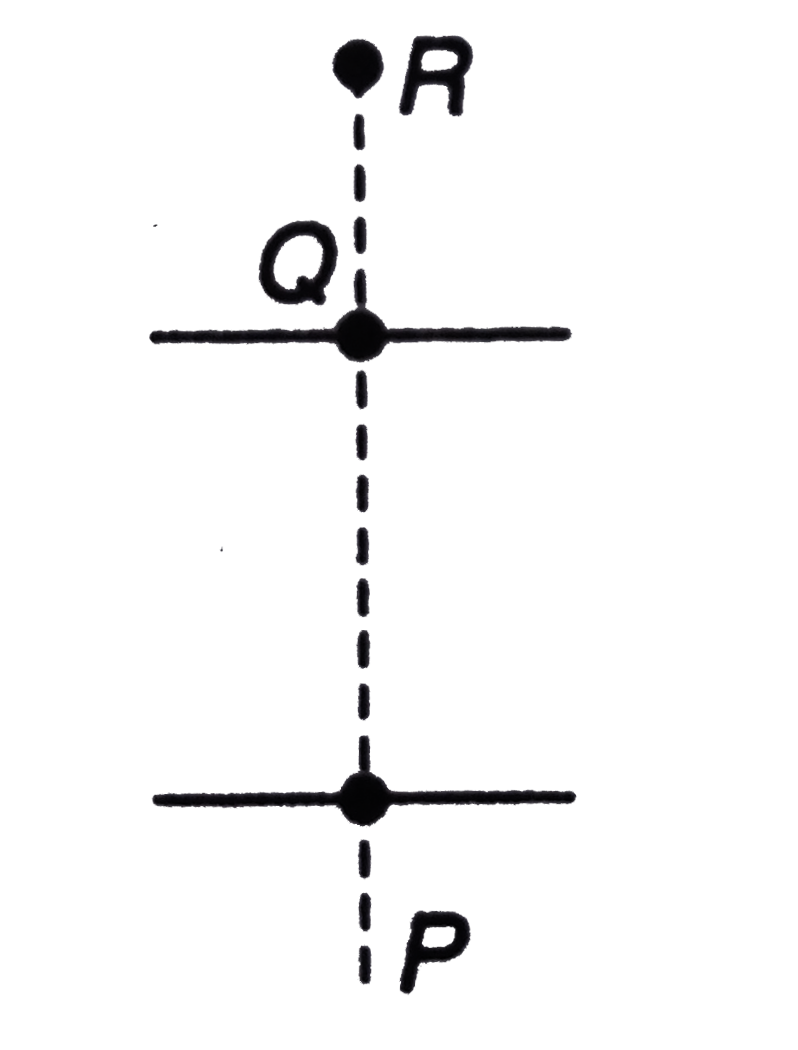
View SolutionA river of width ω is flowing with a uniform velocity v. A boat starts moving from point P also With velocity v relative to the river. The direction of resultant velocity is always perpendicular to the line joining boat and the fixed point R. Point Q is on the opposite side of the river. P, Q and R are in a straight line. If PQ=QR=ω, find (a) the trajectory of the boat, (b) the drifting of the boat and (c) the time taken by the boat to cross the river.
View SolutionA 400 m wide river is flowing from west to east at velocity 3m/s. A boat starts from one bank and it crosses the river along the shortest path. When it reaches the middle of river, wind starts blowing horizontally along north-east at a velocity √2 m/s . Due to this, the direction of rowing of boat has to be changed for the boat to move along the shortest path. If the velocity of boat in still water with no wind blowing is 5 m/s, then choose the correct option(s).
View SolutionA river is flowing with velocity 5km/hr as shown in the figure. A boat start from A and reaches the other bank by covering shortest possible distance. Velocity of boat in still water is 3km/hr. The distance boat covers is.

View Solution
