¯¯¯¯¯¯¯¯MN সরলরেখাংশের বহিঃস্থ বিন্দু P থেকে ¯¯¯¯¯¯¯¯MN সরলরেখাংশের উপর বা বর্ধিত ¯¯¯¯¯¯¯¯MN সরলরেখাংশের উপর লম্ব অঙ্কন করো |
Step by step video & image solution for overline(MN) সরলরেখাংশের বহিঃস্থ বিন্দু P থেকে overline(MN) সরলরেখাংশের উপর বা বর্ধিত overline(MN) সরলরেখাংশের উপর লম্ব অঙ্কন করো | by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- জ্যামিতিBOOK - CHAAYA PRAKASHINI (BENGALI)CHAPTER - জ্যামিতিEXERCISE - EXERCISE
12 Videos
- চতুর্ভুজের শ্রেণিবিভাগBOOK - CHAAYA PRAKASHINI (BENGALI)CHAPTER - চতুর্ভুজের শ্রেণিবিভাগEXERCISE - EXERCISE
14 Videos
- ত্রিভুজ অঙ্কনBOOK - CHAAYA PRAKASHINI (BENGALI)CHAPTER - ত্রিভুজ অঙ্কনEXERCISE - EXERCISE
21 Videos
Similar Questions
স্কেল ও পেনসিলের সাহায্যে PQ একটি 9 সেমি দৈর্ঘ্যের সরলরেখাংশ আঁকো। এই সরলরেখাংশকে সমদ্বিখণ্ডিত করে ‘প্রতি ভাগের দৈর্ঘ্য লেখো।
View Solutionত্রিভুজের বাহুর সংখ্যা 3টি। কর্ণের সংখ্যা □টি ?
View Solutionত্রিভুজের তিনটি বাহুর দৈর্ঘ্য দেওয়া আছে | যদি ত্রিভুজ আঁকা সম্ভব তবে ত্রিভুজ আঁকার চেষ্টা করো ও আর যদি ত্রিভুজ আঁকা সম্ভব নয় তবে কারণ দেখাও : 9 সেমি , 4 সেমি ও 4 সেমি
View Solutionरेखा ¯¯¯¯¯¯AB है तथा इस पर कुछ बिन्दु अंकित है। चित्र की सहायता से निम्न प्रश्नों का सत्य एवं असत्य के अनुसार उत्तर दीजिए ।
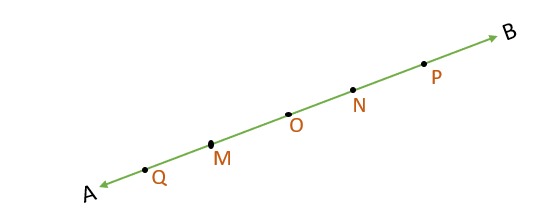
(a) Q,M,O,N और P रेखा ¯¯¯¯¯¯¯¯MN पर स्थित बिंदु है।
(b) M, O और N रेखाखण्ड ¯¯¯¯¯¯¯¯MN के अंतः बिंदु या पर स्थित बिन्दु है।
(c) M और N रेखाखण्ड ¯¯¯¯¯¯¯¯MN के अंत बिंदु है।
(d) O और N रेखाखण्ड ¯¯¯¯¯¯OP के अंत बिंदु है।
(e) M, रेखाखण्ड ¯¯¯¯¯¯QO का अंत बिदु में से एक बिंदु है।
(f) M, किरण ¯¯¯¯¯¯OP पर एक बिंदु है।
(g) किरण ¯¯¯¯¯¯OP, किरण ¯¯¯¯¯¯QP से भिन्न है।
(h) किरण ¯¯¯¯¯¯OP वही है जो किरण ¯¯¯¯¯¯¯OM है ।
(i) किरण ¯¯¯¯¯¯¯OM, किरण ¯¯¯¯¯¯OP के विपरीत (Opposite) नहीं है।
(j) O किरण ¯¯¯¯¯¯OP का प्रारभिक बिंदु नहीं है।
(k) N किरण ¯¯¯¯¯¯NP और ¯¯¯¯¯¯¯¯NM का प्रारंभिक बिंदु है।
View SolutionThe value of ∣∣ ∣ ∣∣¯a⋅¯a¯a⋅¯b¯a⋅¯c¯b⋅¯a¯b⋅¯b¯b⋅¯c¯c⋅¯a¯c⋅¯b¯c⋅¯c∣∣ ∣ ∣∣=
View SolutionIf ¯a,¯b,¯c are three coplanar vectors, the ∣∣ ∣ ∣∣¯a¯b¯c¯a⋅¯a¯a⋅¯b¯a⋅¯c¯b⋅¯a¯b⋅¯b¯b⋅¯c∣∣ ∣ ∣∣=
View SolutionIf ¯a,¯b,¯c are non-coplanar vectors and the vectors ¯p=−¯a+3¯b−5¯c,¯q=−¯a+¯b+¯cand¯r=2¯a−3¯b+¯c are coplanar such that ¯p=m¯q+n¯r, then
View Solution[¯a−¯b¯b−¯c¯c−¯a]=
View Solution[¯a+¯b¯b+¯c¯c+¯a]=
View Solution[¯a¯b+¯c¯c+¯b+¯a]=
View SolutionIf [¯a¯b¯c]=12, then [¯a+¯b¯b+¯c¯c+¯a]=
View SolutionIf [3¯a+5¯b¯c¯d]=p[¯a¯c¯d]+q[¯b¯c¯d], then p+q=
View SolutionIf ¯a,¯band¯c are non-coplanar and (¯a+2¯b−¯c)⋅((¯a−¯b)×(¯a+¯b−¯c))=λ[¯a¯b¯c] then λ=
View SolutionIf ¯a,¯b,¯c are three non-coplanar vectors and ¯p,¯q,¯r are vectors defined by the relations ¯p=¯bׯc[¯a¯b¯c],¯q=¯cׯa[¯a¯b¯c],¯r=¯aׯb[¯a¯b¯c], then (¯a+¯b)⋅¯p+(¯b+¯c)⋅¯q+(¯c+¯a)⋅¯r=
View SolutionIf ¯p=¯bׯc[¯a¯b¯c],¯q=¯cׯa[¯a¯b¯c],¯r=¯aׯb[¯a¯b¯c], where ¯a,¯b,¯c are three non-coplanar vectors, then (¯a+¯b+¯c)⋅(¯p+¯q+¯r)=
View SolutionIf ¯p=¯bׯc[¯a¯b¯c],¯q=¯cׯa[¯a¯b¯c],¯r=¯aׯb[¯a¯b¯c], where ¯a,¯b,¯c are three non-coplanar vectors, then (¯a−¯b−¯c)⋅¯p−(¯b−¯c−¯a)⋅¯q−(¯c−¯a−¯b)⋅¯r=
View Solution
