নীচের সমীকরণটি সমাধান করো : 6(7−3x)+12x=0
Step by step video & image solution for নীচের সমীকরণটি সমাধান করো : 6(7-3x)+12x=0 by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- সমীকরণ গঠন ও সমাধানBOOK - CHAAYA PRAKASHINI (BENGALI)CHAPTER - সমীকরণ গঠন ও সমাধানEXERCISE - EXERCISE
46 Videos
- সমানুপাত ও ঐকিক নিয়মBOOK - CHAAYA PRAKASHINI (BENGALI)CHAPTER - সমানুপাত ও ঐকিক নিয়মEXERCISE - EXERCISE
15 Videos
- সর্বসমতার ধারণাBOOK - CHAAYA PRAKASHINI (BENGALI)CHAPTER - সর্বসমতার ধারণাEXERCISE - EXERCISE
4 Videos
Similar Questions
সমীকরণ তৈরি করো - 33 টি কাঠি দিয়ে x টি সজ্জা
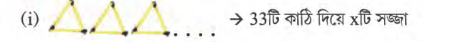
View Solutionসমান গতিবেগে একটি ট্যাক্সি 6ঘণ্টা 12মিনিটে 217কিমি যায়| 273কিমি যেতে ট্যাক্সির কত সময় লাগবে হিসাব করো|
View Solutionদুটি ত্রিভুজের তিনটি কোণের পরিমাপ সমান হলে ত্রিভুজ দুটি সর্বসম হবে কিনা দেখো |
View SolutionFind the equation of the bisector of the obtuse angle between the lines 3x−4y+7=0 and 12x+5y−2=0.
View Solutionदो रेखाओं 3x−4y+7=0 तथा 12x+5y−2=0 के कोण अर्द्धकों का समीकरण होगा।
View Solutionरेखाओं 3x - 4y + 7 = 0 तथा 12x + 5y -2 = 0 के बीच के न्यूनकोण के अर्ध्दक का समीकरण निकालें।
View SolutionWhat are the solutions to 3x2+12x+6=0 ?
View SolutionThe distance between the parallel planes 12x – 3y + 4z – 7 = 0, 12x – 3y + 4z +6 = 0) is
View SolutionThe equations of the lines passing through (4, 5) and making equal angles with the lines 3x=4y+7,5y=12x+6 are
View SolutionThe equations of the bisectors of the angles between the straight line 3x−4y+7=0 and 12x−5y−8=0, are:
View Solutionনীচের সমীকরণটি সমাধান করো : 6(7−3x)+12x=0
View SolutionThe equation of the bisector of the greater angle between the lines 3x-4y + 7 = 0 and -12x-by + 2 = 0 is
View Solutionरेखाओं 3x-4y+ 7 = 0 व 12x+ 5y-2 = 0 के बीच के न्यून कोण के समद्विभाजक का समीकरण है
View Solutionरेखा 3x-4y+ 7 = 0 तथा 12x + 5y-2 =0 के न्यून कोण का कोण समद्विभाजक है
View SolutionLines 3x +4y -7 =0 and 12x +5y +17 =0 Is the equation of the corner between
View Solution
