নীচের সমীকরণগুলির বীজ খোঁজো (সমাধান করো ) : 3(y−5)2+5y=(2y−3)2−(y+1)2+1
Step by step video & image solution for নীচের সমীকরণগুলির বীজ খোঁজো (সমাধান করো ) : 3(y-5)^2+5y=(2y-3)^2-(y+1)^2+1 by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Topper's Solved these Questions
- BOOK - CHAAYA PRAKASHINI (BENGALI)CHAPTER - সমীকরণ গঠন ও সমাধানEXERCISE - EXERCISE23videos
সমীকরণ গঠন ও সমাধান
- BOOK - CHAAYA PRAKASHINI (BENGALI)CHAPTER - সমান্তরাল সরলরেখা ও ছেদকের ধর্মEXERCISE - EXERCISE7videos
সমান্তরাল সরলরেখা ও ছেদকের ধর্ম
- BOOK - CHAAYA PRAKASHINI (BENGALI)CHAPTER - সময় ও কার্যEXERCISE - EXERCISE25videos
সময় ও কার্য
Similar Questions
নীচের সমীকরণগুলির বীজ খোঁজো (সমাধান করো ) : 3x+3=5x+2
05:01View SolutionAB∣∣CD হলে নীচের কোণগুলির মান লেখো- x= ,y=
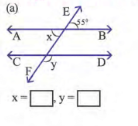 05:35View Solution
05:35View Solutionআমাদের কারখানায় 3 দিনে 216 টি যন্ত্রাংশ তৈরি হয় | 7 দিনে ওই কারখানায় কতগুলি যন্ত্রাংশ তৈরি হবে হিসাব করে লেখো |
02:39View Solution(13y2−47y+5)−(27y−23y2+2)−(17y−3+2y2)
04:29View SolutionAdd the following algebraic expressions: 2,2y3−5y23+5y32,−43+2y23−y2,5y33+3y2+3y+65
07:36View SolutionSubtract :
5y4−3y3+2y2+y−1 from 4y4−2y3−6y2−y+501:39View Solution6(y−32y+1)+1=5√y−32y+1,y≠12:
04:35View Solutionনীচের সমীকরণগুলির বীজ খোঁজো (সমাধান করো ) : 3(y−5)2+5y=(2y−3)2−(y+1)2+1
06:44View SolutionOn dividing 5y3−2y2−7y+1 by y, what will be the remainder ?
05:57View SolutionThe equation of the transvers and conjugate axes of a hyperbola are, respectively, x+2y−3=0 and 2x−y+4=0 , and their respective lengths are √2 and 2√3. The equation of the hyperbola is
a) 25(x+2y−3)2−35(2x−y+4)2=1
b) 25(x−y−4)2−35(x+2y−3)2=1
c)25(2x−y+4)2−35(x+2y−3)2=1
d)2(x+2y−3)2−3(2x−y+4)2=105:41View SolutionAdd the following algebraic expressions: 2,2y3−5y23+5y32,−43+2y23−y2,5y33+3y2+3y+65
01:55View SolutionDivide: 3y4−3y3−4y2−4y2−4y−by y2−2y 2y5+10y4+6y3+y2+5y+3 by 2y3+1
07:08View SolutionLet's find the roots of the equations
3(y−5)2+5y=(2y−3)2−(y+1)2+103:20View SolutionFind the value of the polynomial: y3−5y−2y2+3 when y=2 and y=-2
05:35View SolutionThe equation of the transvers and conjugate axes of a hyperbola are, respectively, x+2y-3=0 and 2x-y+4=0 , and their respective lengths are sqrt(2) and 2/sqrt(3)dot The equation of the hyperbola is a) 2/5(x+2y-3)^2-3/5(2x-y+4)^2=1 b) 2/5(x-y-4)^2-3/5(x+2y-3)^2=1 c) 2/5(2x-y+4)^2-3/5(x+2y-3)^2=1 d) 2(x+2y-3)^2-3(2x-y+4)^2=1
06:17View Solution
