किसी परीक्षण केA,B,C तथा D, चार संभव परिणाम हैं, जो परस्पर अपवर्जी हैं। स्पष्ट कीजिए कि प्रायिकता का निम्नलिखित निर्धारण, अनुज्ञेय (permissible) क्यों नहीं है
(a) P(A) = .12, P(B) = .63, P(C ) = 0.45, P(D) = - 0.20
(B) P(A) = 9/120, P(B) =45/120, P(C ) = 27/120,
P(D) = 46/120
The correct Answer is:127120≠1
Step by step video, text & image solution for किसी परीक्षण केA,B,C तथा D, चार संभव परिणाम हैं, जो परस्पर अपवर्जी हैं। स्पष्ट कीजिए कि प्रायिकता का निम्नलिखित निर्धारण, अनुज्ञेय (permissible) क्यों नहीं है (a) P(A) = .12, P(B) = .63, P(C ) = 0.45, P(D) = - 0.20 (B) P(A) = 9/120, P(B) =45/120, P(C ) = 27/120, P(D) = 46/120 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- प्रायिकताBOOK - NCERT EXEMPLAR HINDICHAPTER - प्रायिकताEXERCISE - उदहारण -दीर्घउत्तरीय
1 Videos
- प्रायिकताBOOK - NCERT EXEMPLAR HINDICHAPTER - प्रायिकताEXERCISE - उदहारण -वस्तुनिष्ठ प्रश्न
7 Videos
- द्विपद प्रमेय BOOK - NCERT EXEMPLAR HINDICHAPTER - द्विपद प्रमेय EXERCISE - 8.3 प्रश्नावली (सत्य या असत्य)
7 Videos
- रैखिक असमिकाएँ BOOK - NCERT EXEMPLAR HINDICHAPTER - रैखिक असमिकाएँ EXERCISE - 6.3 प्रश्नावली (सत्य हैं या असत्य)
15 Videos
Similar Questions
एक कलश में 1 से 20 तक क्रमांकित कागज़ की बीस सफेद पर्चियाँ, 1 से 10 तक क्रमांकित कागज की दस लाल पर्चियाँ, । से 40 तक क्रमांकित कागज़ की चालीस पीली पर्चियाँ तथा 1 से 10 तक क्रमांकित कागज की दस नीली पर्चियाँ हैं। यदि कागज की ये 80 पर्चियाँ अच्छी तरह से मिला दी गई हों, जिससे प्रत्येक पर्ची के कलश से निकाले जाने की प्रायिकता समान हो, तो एक पर्ची के निकालने की निम्नलिखित प्रायिकताएँ ज्ञात कीजिए:
(a) पर्ची नीली या सफ़ेद हो
(b) पर्ची 1, 2, 3, 4 या 5 क्रमांकित हो
(c) पर्ची लाल या पीली हो और 1, 2, 3 या 4 क्रमांकित हो
(d) पर्ची 5, 15, 25,या 35 क्रमांकित हो
(e) पर्ची सफेद हो और उस पर 12 से अधिक संख्या अंकित हो या पर्ची पीली हो और उस पर 26 से अधिक संख्या अंकित हो।
View Solutionकिसी लीप वर्ष (Leap year) में 53 रविवार या 53 सोमवार होने की प्रायिकता है:
View Solutionश्रेणी 10∑r=020Cr, का योग 219+20C102 है।
View Solutionयदि x<y और b<0 तो xb<yb
View SolutionIf A and B are any two events such that P(A)+P(B)−P(AandB)=P(A)? then
(A) P(B∣A)=1
(B) P(A∣B)=1
(C) P(B∣A)=0
(D) P(A∣B)=0
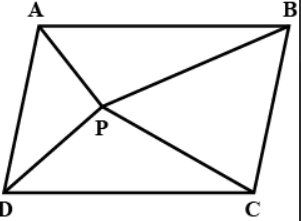
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View SolutionIf A and B are arbitrary events,then a )P(A nn B)>=P(A)+P(B)(b)P(A uu B)<=P(A)+P(B)(c)P(A nn B)=P(A)+P(B)(d) (d)None of these
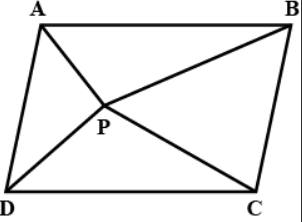
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)
View SolutionABCD is a cyclic quadrilateral whose diagonals AC and BD intersect at P. If AB=DC, prove that:
(i)PAB ≅PDC
(ii)PA=PD and PC=PB (iii) AD∣∣BC
View SolutionIf P((A)/(C))>P((B)/(C)) and P((A)/(bar(C)))>P((B)/(bar(C))), then the relationship between P(A) and P(B) is (A)P(A)=P(B) (B) P(A) P(B)(D)P(A)>=P(B)
View Solutionदो घटनाएँ A तथा B परस्पर स्वतंत्र खलती हैं यदि (क) P(A)=P(B) (ख) P(A)+P(B)=1 (ग) P(bar AB)=[1- P(A)][1- P(B)] (घ) A और B परस्पर अपवर्जी है।
View Solutionदो घटनाएँ A तथा B परस्पर स्वतंत्र कहलाती है यदि
(a) P(P(A))=P(B) (b ) P(A)+P(B)=1
(c ) P(¯¯¯A¯¯¯B)=[1−P(A)][1−P(B)]
(d ) A और B परस्पर अपवर्जी है
View SolutionAn experiment has four possible outcomes A, B, C and D that are multually exclusive. Explain why the following assignments of porbability are not permissible,
a. P(A)=0.12,P(B)=0.63,P(C)=0.45,P(D)=−0.20
b. P(A)=9120,P(B)=45120,P(C)=27120,P(D)=46120
View SolutionAn experiment has four possible outcomes. A,B,C and D that are mutually exclusive. Explain why the following assignments of probability are not permissible
(i) P(A)=0.12,P(B)=0.63,P(C)=0.45,P(D)=−0.20
(ii) P(a)+9120,P(B)=45120,P(C)=27120,P(D)=46120
View SolutionIf A and B are any two events such that P(A)+P(B)−P(AandB)=P(A)? then(A) P(B∣A)=1 (B) P(A∣B)=1(C) P(B∣A)=0 (D) P(A∣B)=0
View SolutionFor positive real numbers a,bc such that a+b+c=p, which one holds? (a) (p−a)(p−b)(p−c)≤827p3 (b)(p−a)(p−b)(p−c)≥8abc (c)bca+cab+abc≤p (d) none of these
View Solution
