A regular tetrahedron is obtaining during _____hybridisation in alkanes.Solution in Odia
The correct Answer is:sp3
Step by step video, text & image solution for A regular tetrahedron is obtaining during _____hybridisation in alkanes. by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
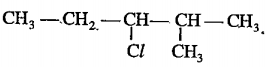
Give IUPAC name of :
View SolutionName an isotope of hydrogen.
View SolutionLet k be the length of any edge of a regular tetrahedron (a tetrahedron whose edges are equal in length is called a regular tetrahedron). Show that the angle between any edge and a face not containing the edge iscos−1(1/√3) .
View SolutionIf the edge of a regular tetrahedron is 1cm, then its volume is
View SolutionRegular tetrahedron a tetrahedron whose all the edges are of equal length is called a regular tetrahedron.
View SolutionIn phenyl isocyanide the carbons are _____hybridised.
View SolutionThe acute angle betwene any two faces of a regular tetrahedron is
View SolutionLet OABC be a regular tetrahedron with side length unity, then its volume (in cubic units) is
View SolutionThe corrners of regular tetrahedrons are number 1,2,3,4. Three tetrahedrons are tossed . The probability that the sum of upward corners will be 5 is .
View SolutionOABC is a regular tetrahedron of side unity, then:
View SolutionLet k be the length of any edge of a regular tetrahedron (a tetrahedron whose edges are equal in length is called a regular tetrahedron). Show that the angel between any edge and a face not containing the edge iscos−1(1/√3) .
View SolutionLet k be the length of any edge of a regular tetrahedron (a tetrahedron whose edges are equal in length is called a regular tetrahedron). Show that the angel between any edge and a face not containing the edge iscos−1(1/√3) .
View SolutionDraw the net of a regular tetrahedron with side 6 cm.
View SolutionLet k be the length of any edge of a regular tetrahedron (a tetrahedron whose edges are equal in length is called a regular tetrahedron). Show that the angle between any edge and a face not containing the edge is cos^(-1)(1//sqrt(3)) .
View SolutionThe corners of regular tetrahedrons are numbered 1, 2, 3, 4. Three tetrahedrons are tossed. The probability that sum of upward corners will be 5 is
View Solution
