Concrete blocks of masses mA and mB are balanced on two identical vertical springs mA=2mB . The gravitational potential energy of each system is zero at the equilibrium position of the springs. Which statements is true for the total mechanical energy of the systems when the blocks are balanced on the springs?
EA=EB
EA=2EB
EA=4EB
EA=−2EB
The correct Answer is:C
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - MTG GUIDECHAPTER - WORK, ENERGY AND POWEREXERCISE - AIPMT/NEET (MCQs)
34 Videos
- WORK, ENERGY AND POWERBOOK - MTG GUIDECHAPTER - WORK, ENERGY AND POWEREXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS) (COLLISIONS)
35 Videos
- THERMODYNAMICSBOOK - MTG GUIDECHAPTER - THERMODYNAMICSEXERCISE - AIPMT/NEET (MCQs)
26 Videos
Similar Questions
In figure, k=100N/m,M=1kg and F=10N

(a) Find the compression of the spring in the equilibrium position
(b) A sharp blow by some external agent imparts a speed of 2m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
(c) Find the time period of the resulting simple harmonic motion.
(d) Find the amplitude.
(e) Write the potential energy of the spring when the block is at the left estreme.
(f) Write the potential energy of the spring when the block is at the right extreme.
The answers of (b), (e) and (f) are different. Explain why this does not violate the principle of conservation of energy ?
View SolutionIn figure, k=100N/m,M=1kg and F=10N

(a) Find the compression of the spring in the equilibrium position
(b) A sharp blow by some external agent imparts a speed of 2m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
(c) Find the time period of the resulting simple harmonic motion.
(d) Find the amplitude.
(e) Write the potential energy of the spring when the block is at the left estreme.
(f) Write the potential energy of the spring when the block is at the right extreme.
The answers of (b), (e) and (f) are different. Explain why this does not violate the principle of conservation of energy ?
View Solution
Knowledge Check
Concerete block of mass mAandmB. The gravitutional potential energy of each system is zero at the equilibrium position of the springs. Which ststement is true for the total machanical energy of the springs. Which system when the block , are balanced on the springs?
AEA=EBBEA=2EBCEA=4EBDEA=−2EBTwo blocks of masses m1 and m2 are attached to the lower end of a light vertical spring of force constant k. The upper end of the spring is fixed. When the system is in equilibrium, the lower block (m2) drops off. The other block (m1) will
 Aremain undistrubedBmove through a distance m2gk and come to restCundergo vertical SHM with a time period of 2π√m1kDundergo vertical SHM with a time period of
Aremain undistrubedBmove through a distance m2gk and come to restCundergo vertical SHM with a time period of 2π√m1kDundergo vertical SHM with a time period of
2π√m1+m2k
Two blocks A and B of masses mA and mB are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Show that the kinetic energies of the blocks are, at any instant inversely proportional to their masses.
View SolutionTwo blocks A and B of masses mA and mB are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Show that the kinetic energies of the blocks are, at any instant inversely proportional to their masses.
View SolutionSpring mass system is shown in figure. Find the elastic potential energy stored in each spring when block is at its mean position. Also find the time period of vertical oscillations. The system is in vertical plane.

View SolutionSpring mass system is shown in figure. Find the elastic potential energy stored in each spring when block is at its mean position. Also find the time period of vertical oscillations. The system is in vertical plane.

View SolutionA light spring is vertical and a mass less pan is attached to it. Force constant of the spring is k. A block of mass m is gently dropped on the pan. Plot the variation of spring potential energy, gravitation potential energy and the total potential energy of the system as a function of displacement (x) of the block. For gravitational potential energy take referece level to the initial postion of the pan.
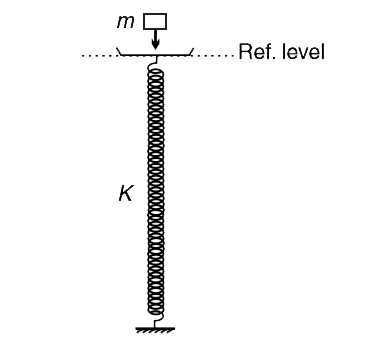
View SolutionTwo blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length. A third identical block C also of mass m moves on the floor with a speed v along the line joining A and B and collides with A. Then
The kinetic energy of the A-B system at maximum compression of the spring is mv2/4
The maximum compression of the spring v√m/3k<br>Thek∈etice≠rgyoftheA−Bsystematmaxiμmcompression<br>Themaxiμmcoppressionofthespr∈gisvsqrt(m//k)
View Solution
