Street Plan : A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction. All other streets of the city run parallel to these roads and are 200 m apart. There are about 5 streets in each direction. Using 1 cm = 200 m, draw a model of the city on your notebook. Represent roads/ streets by single lines. There are many cross-streets in your model. A particular cross-street is made by two streets, one running in the North - South direction and another in the East - West direction. Each cross street is referred to in the following manner : the 2nd street running in the North -South direction and 5th in the East - West direction meet at some crossing, then we will call this crossstreet (2, 5). Using this convention find : how many cross-streets can be referred to as (3, 4).
Step by step video & image solution for Street Plan : A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction. All other streets of the city run parallel to these roads and are 200 m apart. There are about 5 streets in each direction. Using 1 cm = 200 m, draw a model of the city on your notebook. Represent roads/ streets by single lines. There are many cross-streets in your model. A particular cross-street is made by two streets, one running in the North - South direction and another in the East - West direction. Each cross street is referred to in the following manner : the 2^(nd) street running in the North -South direction and 5^(th) in the East - West direction meet at some crossing, then we will call this crossstreet (2, 5). Using this convention find : how many cross-streets can be referred to as (3, 4). by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
ರಸ್ತೆ ಯೋಜನೆ : ನಗರದ ಮಧ್ಯಭಾಗದಲ್ಲಿ ಒಂದನ್ನೊಂದು ಅಡ್ಡ ಹಾದುಹೋಗದ೦ತ ಒಂದು ನಗರದಲ್ಲಿ ಎರಡು ಮುಖ್ಯರಸ್ತೆಗಳಿವೆ. ಈ ಎರಡು ರಸ್ತೆಗಳೂ ಒಂದು ಉತ್ತ -. ದಕ್ಷಿಣ ದಿಕ್ಕಿನಲ್ಲೂ ಇನ್ನೊಂದು ಮೂರ್ವ - ಪಶ್ಚಿಮ ದಿಕ್ಕಿನಲ್ಲೂ ಇವೆ. ಪರಸರ 200 m ಅಂತರದಲ್ಲಿರುವ ಇತರ ನಗರದ ಎಲ್ಲಾ ರಸ್ತೆಗಳೂ ಈ ರಸ್ತೆ ಸಮಾಂತರವಾಗಿದೆ. ಪ್ರತಿಯೊಂದು ದಿಕ್ಕಿನಲ್ಲೂ 5 ರಸ್ತೆಗಳಿವೆ. 1cm= 200m, ಎ೦ಬ ಪ್ರಮಾಣವನ್ನು ಉಪಯೋಗಿಸಿ ನಿಮ್ಮ ನೋಟ್ ಪುಸ್ತಕದಲ್ಲಿ ನಗರದ ಒಂದು ಮಾದರಿ ನಕ್ಷೆಯನ್ನು ರಚಿಸಿ. ರಸ್ತೆ/ಅಡ್ಡರಸ್ತೆಗಳನ್ನು ಏಕರೇಖೆಗಳಿಂದ ಪ್ರತಿನಿಧಿಸಿ. ನಿಮ್ಮ ಮಾದರಿಯಲಲಿ ಅನೇಕ ಛೇದಿಸುವ ರಸ್ತೆಗಳಿವೆ. ಇಂತಹ ಪ್ರತಿಯೊಂದು ಜೂತೆ ಛೇದಿಸುವ ರಸ್ತೆಗಳು, ಒಂದು ಉತ್ತರ - ದಕ್ಷಿಣ ದಿಕ್ಕು ಮತ್ತು ಇನ್ನೊಂದು ಪೂರ್ವ - ಪಶ್ಚಿಮ ದಿಕ್ಕಿನಲ್ಲಿರುವ ಎರಡು ರಸ್ತೆಗಳಿಂದ ಉಂಟಾಗಿವೆ. ಪ್ರತಿಯೊಂದು ಜೊತೆ ಛೇದಿಸುವ ರಸ್ತೆಗಳನ್ನೂ ಈ ಮುಂದಿನ ಕ್ರಮದಲ್ಲಿ ಆದರಿಸಬಹುದು. ಉತ್ತರ -. ದಕ್ಷಿಣ ದಿಕ್ಕಿನಲ್ಲಿರುವ 2ನೇಯ ರಸ್ತೆ ಮತ್ತು ಪೂರ್ವ - ಪಶ್ಚಿಮ ದಿಕ್ಕಿನಲ್ಲಿರುವ 5ನೆಯ ರಸ್ತೆಗಳು ಒಂದನ್ನೊಂದು ಸಂಧಿಸುವ ಸ್ಥಾನವನ್ನು ನಾವು ರಸ್ತೆ ಛೇದನ (2, 5) ಎಂದು ಕರೆಯುತ್ತೇವೆ. ಈ ಪದ್ಧತಿಯನ್ನು ಉಪಯೋಗಿಸಿ. (ii) (3, 4) ಎಂದು ಎಷ್ಟು ರಸ್ತೆ ಛೇದನಗಳನ್ನು ಉಲ್ಲೇಖಿಸಬಹುದು? - ಎಂಬುದನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
View SolutionThe streets of a city are arranged like the like the lines of a chess board. There are m streets running from north to south and n streets from east to west. Find the number of ways in which a man can travel from north-west to south-east corner, covering shortest possible distance.
View SolutionManagement city has m parallel roads running East-West and n parallel roads running North-South. How many shortest possible routes are possible to go from one corner of the city to its diagonally opposite corner?
View SolutionIn a locality, there is a main road along North-South direction. The map is given below. With the help of the pic ture answer the following questions. (Start from main road to different street and head should be in east) : What is there on the 3rd place on the left side in street no. 3 ?
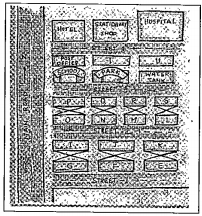
View SolutionIn a locality, there is a main road along North-South direction. The map is given below. With the help of the pic ture answer the following questions. (Start from main road to different street and head should be in east) : Find the name of the 2nd house which is in right side of street 2.
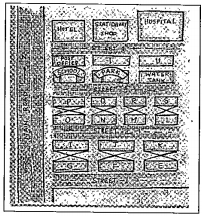
View Solution(सड़क योजना): एक नगर में दो मुख्य सड़कें हैं, जो नगर के केंद्र पर मिलती हैं। ये दो सड़कें उत्तर-दक्षिण की दिशा और पूर्व-पश्चिम की दिशा में हैं। नगर की अन्य सभी सड़कें इन मुख्य सड़कों के समांतर परस्पर 200 मीटर की दूरी पर हैं। प्रत्येक दिशा में लगभग पांच सड़कें हैं। 1 सेंटीमीटर = 200 मीटर का पैमाना लेकर अपनी नोट बुक में नगर का एक मॉडल बनाइए। सड़कों को एकल रेखाओं से निरूपित कीजिए।
आपके मॉडल में एक-दूसरे को काटती हुई अनेक क्रॉस-स्ट्रीट (चौराहे) हो सकती हैं। एक विशेष क्रॉस-स्ट्रीट दो सड़कों से बनी है, जिनमें से एक उत्तर-दक्षिण दिशा में जाती है और दूसरी पूर्व-पश्चिम की दिशा में। प्रत्येक क्रॉस-स्ट्रीट का निर्देशन इस प्रकार किया जाता है : यदि दूसरी सड़क उत्तर-दक्षिण दिशा में जाती है और पांचवीं सड़क पूर्व-पश्चिम दिशा में जाती है और ये एक क्रॉसिंग पर मिलती हैं, तब इसे हम क्रॉस-स्ट्रीट (2,5) कहेंगे। इसी परंपरा से यह ज्ञात कीजिए कि
(i) कितनी क्रॉस-स्ट्रीटों को (4,3) माना जा सकता है।
(ii) कितनी क्रॉस-स्ट्रीटों को (3, 4) माना जा सकता है।
View SolutionThe streets of a city are arranged like the lines of a chess board. There are m streets running from north to south and n streets from east to west. Find the number of ways in which a man can travel from north-west to south-east corner, covering shortest possible distance.
View SolutionThe streets of a city are arranged like the lines of a chess board . There are m streets running North to South and 'n' streets running East to West . The number of ways in which a man can travel from NW to SE corner going the shortest possible distance is
View Solution
