In Fig.
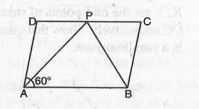 ABCD is a parallelogram in which ∠A=60∘. If the bisector of ∠A and ∠B meet at P prove that AD = DP, PC = BC and DC = 2AD.
ABCD is a parallelogram in which ∠A=60∘. If the bisector of ∠A and ∠B meet at P prove that AD = DP, PC = BC and DC = 2AD.
Step by step video & image solution for In Fig. ABCD is a parallelogram in which /_A = 60^@. If the bisector of /_A and /_B meet at P prove that AD = DP, PC = BC and DC = 2AD. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
The inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionIn Fig, find the value of x.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_S01_032_Q01.png" width="80%"gt
View SolutionAt point P, the value of (dy)/(dx) is : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_025_Q01.png" width="80%"gt
View SolutionIn the given fig. If DE||BC Find EC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/MATH_241_X_SQP_E01_021_Q01.png" width="80%"gt
View SolutionIn the figure, ABCD is a parallelogram, in which /_ A = 60^(@) | If /_ A And /_ B If the bisectors of P meet at P, prove that AD = DP, PC = BC And DC = 2AD
View Solution
