Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method : The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the number. Find the number.Solution in Punjabi
Step by step video & image solution for Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method : The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the number. Find the number. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PAIR OF LINEAR EQUATIONS IN TWO VARIABLESBOOK - MBDCHAPTER - PAIR OF LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - EXERCISE
183 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - MBDCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - EXERCISE
176 Videos
- POLYNOMIALSBOOK - MBDCHAPTER - POLYNOMIALSEXERCISE - EXERCISE
51 Videos
Similar Questions
4 chairs and 3 tables cost ? 2100 and 5 chairs and 2 tables cost ? 1750. Represent this situation algebraically and graphically.
View SolutionIn △ABC, right angled at A, if AB = 12 cm, AC = 5 cm and BC = 13 cm, find all the six trigonometric ratios of angle B.
View SolutionThe graphs of y = p (x) are given in figure below, for some polynomials p (x). Find the number of zeroes of p (x), in each case.
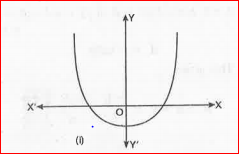 .
.
View SolutionThe sum of the digits of a two-digit number is 9.Also,nine xx this number is twice the number obtained by reversing the order of the digits.Find the number.
View SolutionThe sum of digits of a two digit number is 15. The number obtained by reversing the order of digits of the given number exceeds the given number by 9. Find the given number.
View SolutionThe sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
View Solutionदो अंको की संख्या के अंकों का योग 9 है । इस संख्या का नौ गुना , संख्या से अंकों को पलटने से बनी संख्या का दो गुना है । वह संख्या ज्ञात कीजिए ।
View Solutionसमस्याओ में रेखिक समीकरणों के युग्म बनाइए और उनके हल (यदि उनका अस्तित्व हो ) विलोपन विधि से ज्ञात कीजिए :
दो अको की सख्या के अको का योग 9 है । इस सख्या का नौ गुना , सख्या के अको को पलटने से बनी सख्या का दो गुना है । वह सख्या ज्ञात कीजिए ।
View Solutionदो अंकों वाली संख्या के अंकों का योग 9 है। इस संख्या का 9 गुना, संख्या के अंकों को पलटने पर बनी संख्या को दोगुना है। संख्या ज्ञात कीजिए।
View Solutionनिम्न समस्या में रैखिक समीकरण के युग्म बनाइए और उनके हल ( यदि उनका अस्तित्व हो) विलोपन विधि ज्ञात कीजिए :
दो अंकों की संख्या का योग 9 है । इस संख्या का नौ गुना संख्या के अंकों को पलटने से बनी संख्या का दो गुना है । वह संख्या ज्ञात कीजिए ।
View Solutionनिम्नलिखित समस्याओं के लिए रैखिक समीकरणों के युग्म बनाइए और निराकरण विधि से उनके हल (यदि हों) ज्ञात कीजिए :
(iii) दो अंकों वाली एक संख्या और इसके अंकों को पलटने से प्राप्त संख्या के अंकों का योग 99 है। यदि संख्या में पाँच जोड़ दिया जाए तो यह संख्या के अंकों के योग 6 गुणा से 4 कम होता है। संख्या ज्ञात कीजिए।
View Solutionनिम्नलिखित समस्याओं के लिए रैखिक समीकरणों के युग्म बनाइए और निराकरण विधि से उनके हल (यदि हों) ज्ञात कीजिए :
(iv) दो अंकों वाली संख्या इसके अंकों के योग का तीन गुणा है। यदि इसमें 45 जोड़ दिए जाएं तो इसके अंक पलट जाते हैं। संख्या ज्ञात कीजिए।
View SolutionThe sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
View SolutionThe sum of the digits of a two-digits number is 9. Also nine times this number is twice the number obtained by reserving the order of the digits. Find the number.Solve by cross multiplication method.
View SolutionThe sum of digits of a two digit number is 15. The number obtained by reversing the order of digits of the given number exceeds the given number by 9. Find the given number.
View SolutionThe sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
View Solution
