In an A.P. third term is 14 and 8th term is 34. Find Sn and S20 .Solution in Punjabi
Step by step video & image solution for In an A.P. third term is 14 and 8th term is 34. Find S_n and S_(20) . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find out which of the following sequences are arithmetic progressions. For those which are arithmetic progressions, find out the common difference. :- 3,6,12,24,….
View SolutionA bicycle wheel makes 500 revolutions in moving 11 km. Find the diameter of the wheel.
View SolutionComplete the prime factor tree :
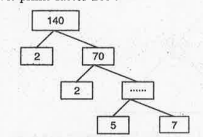
View SolutionFind 8th term of the A.P. 117, 104, 91, 78,
View SolutionThe sum of first 20 terms of an A.P. is one third of the sum of next 20 term. If first term is 1, find the sum of first 30 terms of this A.P.
View SolutionFind the 20th term of an A.P. whose 5th term is 15 and the sum of its 3rd and 8th terms is 34.
View SolutionLet Sn denote the sum of first n terms of an A.P. If S2n=3Sn, then find the ratio S3n/Sn.
View SolutionLet Sn denote the sum of first n terms of an A.P. If S2n=3Sn, then find the ratio S3n/Sn.
View SolutionThe sum of 4th and 8th terms of an A.P. is 24 and the sum of the 6th and 10th terms is 34. Find the first term and the common difference of the A.P.
View SolutionIf Sn denotes the sum of the first n terms of an A.P., prove that S30=3(S20−S10) .
View SolutionLet Sn denotes the sum of the first of n terms of A.P. and S2n=3Sn . then the ratio S3n:Snis equal to
View SolutionThe sum of 4th and 8th terms of an A.P. is 24 and the sum of the 6th and 10th terms is 34. Find the first term and the common difference of the A.P.
View SolutionThe 6th term of an A.P. is 12 and the 8th term is 22, Find the 10th term.
View SolutionThe 8th term of a series in an A.P. is 23 and the 102nd term is 305 . Find the series .
View SolutionIf the 8th term of an A.P. is 37 and the 15th term is 15 more than the 12th find the A.P. Also find the sum of first 20 terms of this A.P.
View Solution
