Area of an equilateral triangle is 17300 cm2. By taking each vertex of the triangle as centre, a circle is drawn at each vertex. The radius of thecircleis half of the length of the side of an equilateral triangle. Find the area of that portion of the triangle which is not included in the circle. (π=3.14 and √3=1.73)Solution in Punjabi
Step by step video & image solution for Area of an equilateral triangle is 17300 cm^2. By taking each vertex of the triangle as centre, a circle is drawn at each vertex. The radius of thecircleis half of the length of the side of an equilateral triangle. Find the area of that portion of the triangle which is not included in the circle. (pi=3.14 and sqrt3=1.73) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A bicycle wheel makes 500 revolutions in moving 11 km. Find the diameter of the wheel.
View SolutionRestate the following statements with appropriate conditions, so that they become true. : The diagonals of a quadrilateral bisect each otther.
View SolutionFind out which of the following sequences are arithmetic progressions. For those which are arithmetic progressions, find out the common difference. :- 3,6,12,24,….
View SolutionThe area of an equilateral ΔABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see the figure). Find the area of the shaded region. [Take π = 3.14 and √3 = 1.73205]
View SolutionThe area of an equilateral triangle is 1732.05 cm2 . About each angular point as centre, a circle is described with radius equal to half the length of the side of the triangle. Find the area of the triangle not included in the circles. (Use π=3.14) .
View SolutionThe area of an equilateral triangle is 100√3cm2. Taking each vertex as centre, a circle is described with radius equal to half the length of the side of the triangle, as shown in the figure. Find the area of that part o the triangle which is not included in the circles.
[Take π=3.14 and √3=1.732]
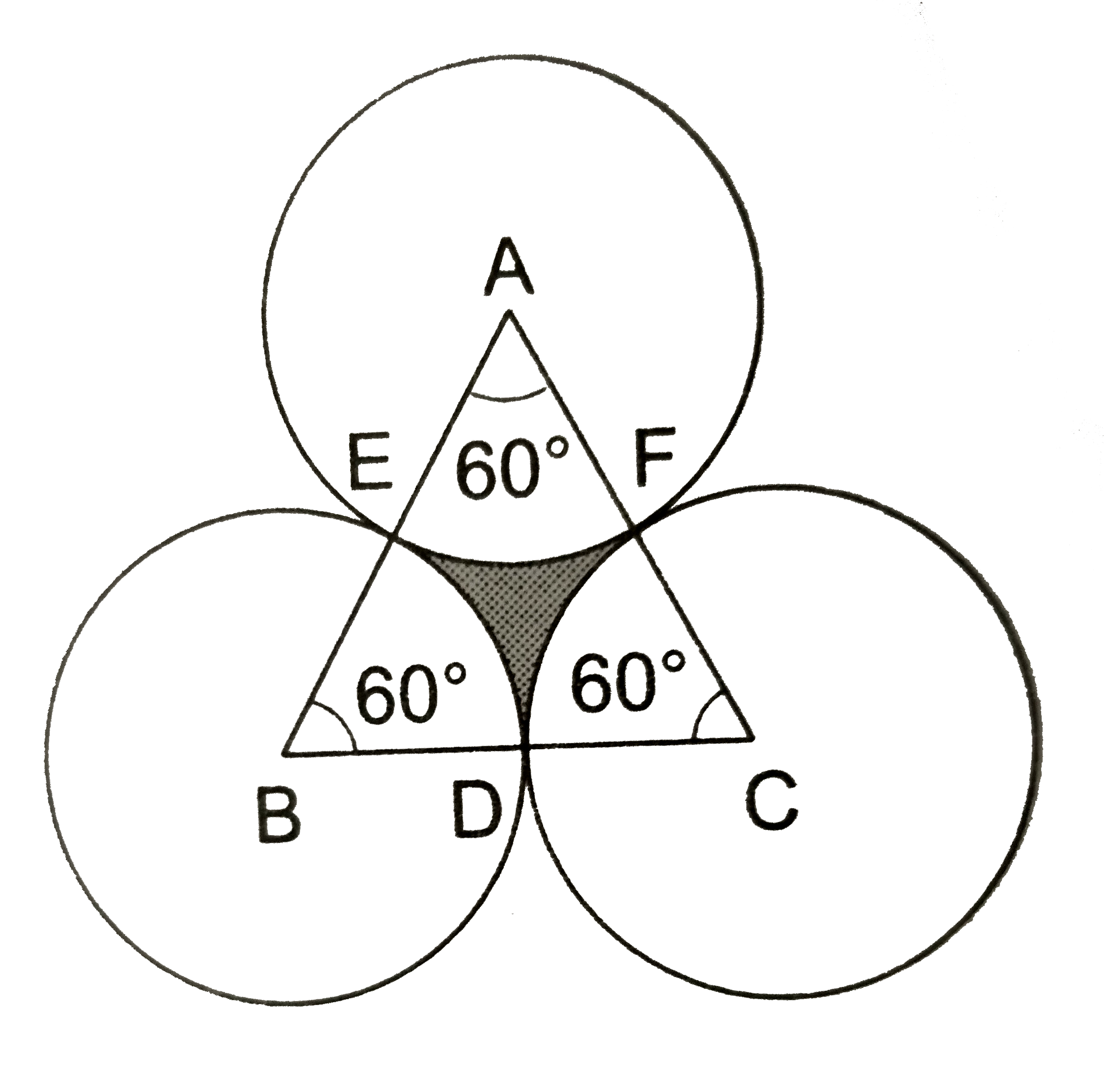
View Solutionएक समबाहु त्रिभुज ABC का क्षेत्रफल 17320.5 cm2 है। इस त्रिभुज के प्रत्येक शीर्ष को केन्द्र मानकर त्रिभुज की भुजा के आधे के बराबर की त्रिज्या लेकर एक वृत्त खींचा जाता है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
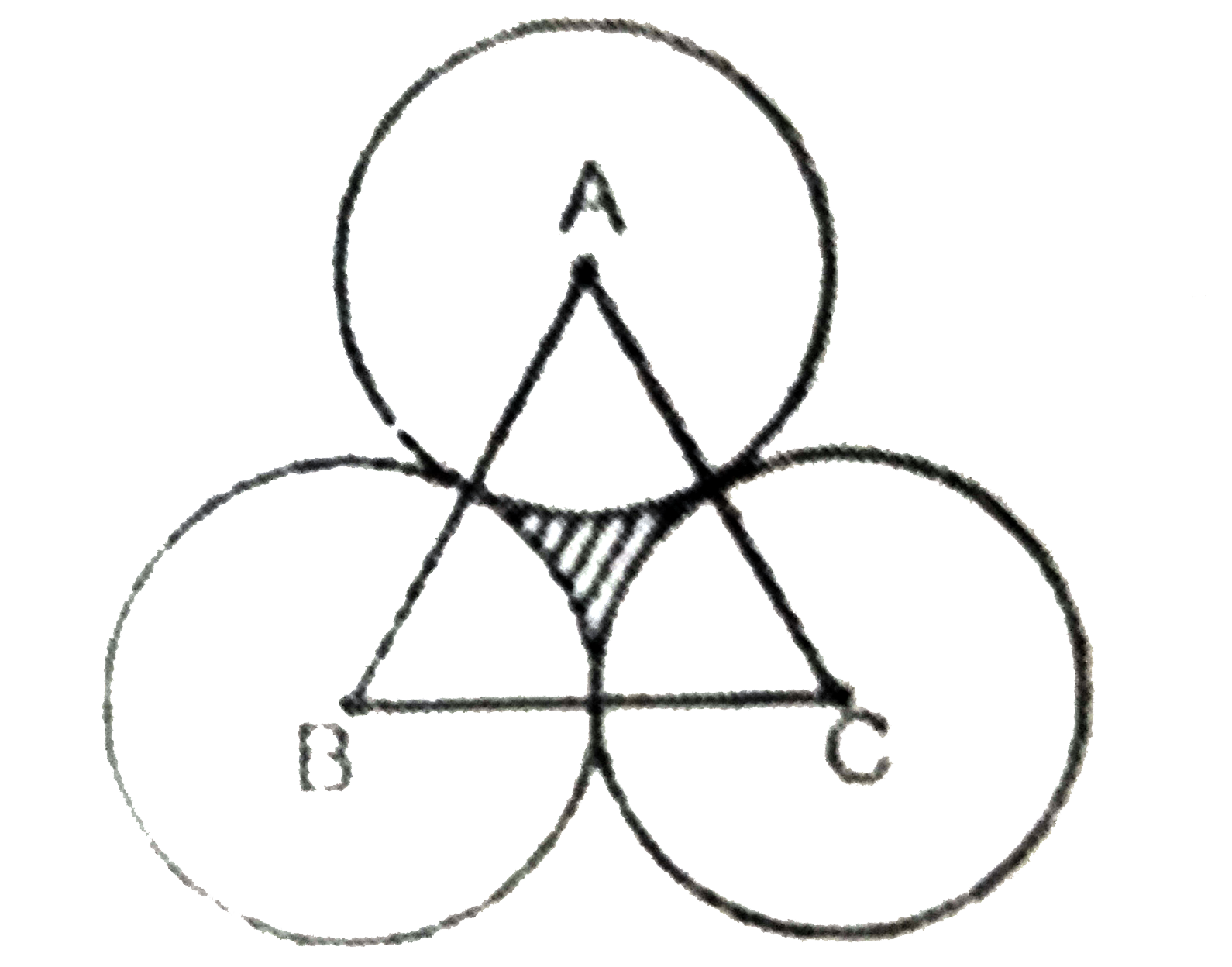
View Solution12 cm भुजा वाले समबाहु त्रिभुज के अंतर्गत एक वृत्त खींची गई है जो त्रिभुज की भुजाओं को स्पर्श करती है। त्रिभुज के उस भाग को क्षेत्रफल ज्ञात करे जो वृत्त से घिरा नहीं है। [√3=1.73 और π=3.14 ले ]
View Solutionएक समबाहु त्रिभुज का क्षेत्रफल 49√3 सेमी.2 है | प्रत्येक शीर्ष को केन्द्र मानकर त्रिभुज की भुजा की लम्बाई की आधी त्रिज्या लेकर वृत्त खींचे गये हैं जैसा कि चित्र में प्रदर्शित किया गया है | त्रिभुज के उस भाग का क्षेत्रफल ज्ञात कीजिये जो वृत्तों में सम्मिलित नहीं है |
View Solutionकिसी समबाहु त्रिभुज के प्रत्येक शीर्ष को केंद्र लेते हुए त्रिभुज की भुजा की आधी लम्बाई को त्रिज्या मानकर एक-एक वृत्त खींचा जाता है| त्रिभुज का जो अंश वृतों के बाहर रहता है
(i) 17320.5 वर्ग सेमी हो (π=3.14,√3=1.73205लें)
(ii) 49√3 वर्ग सेमी हो (π=227,√3=1.73)
View Solutionएक समबाहु त्रिभुज का क्षेत्रफल 17300cm2 है। त्रिभुज के प्रत्येक शीर्ष को केन्द्र लेकर एक वृत्त खींचा गया ह। वृत्त की त्रिज्या समबाहु त्रिभुज की भुजा की लंबाई के आधा है । त्रिभुज के उस भाग का क्षेत्रफल ज्ञात कीजिए जो वृत्त में नहीं है। (π=3.14 और √3=1.73)
View Solutionएक समबाहु त्रिभुज का क्षेत्रफल 49√3cm2 है। प्रत्येक शीर्ष को केंद्र मानकर त्रिभुज की भुजा की लम्बाई की आधी त्रिज्या लेकर वृत्त खींचे गए हैं , जैसा कि संलग्न आकृत्ति में दर्शाया गया है। त्रिभुज के उस भाग का क्षेत्रफल ज्ञात कीजिए जो वृत्तों में सम्मिलित नहीं है। (√3=1.73 लीजिए )

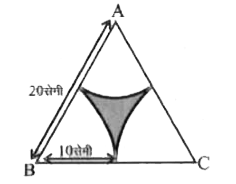
View Solutionचित्र में ABC एक समबाहु त्रिभुज है जिसकी एक भुजा 20 सेमी है। त्रिभुज के प्रत्येक शीर्ष से 10 सेमी त्रिज्या के वृत्त खींचे गये हैं। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (π=3.14 लीजिए)
View SolutionThe area of an equilateral triangle ABC is 17320.5cm2. With each vertex of the trianlge as centre, a circle is drawn with radius equal to half the length of the side of the triangle. Find the area of the shaded region .
View Solutionएक समबाहु त्रिभुज का क्षेत्रफल 100√3 cm2 की भुजा की आधी लम्बाई को त्रिज्या मानकर वृत्त खींचे गए हैं जैसा कि आकृति में दिखाया गया है । त्रिभुज का वह क्षेत्रफल ज्ञात कीजिए जो वृत्तों में शामिल न हो। (√3 = 1.732 "तथा" π = 3.14 "लीजिए।")
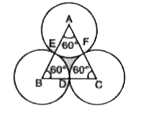
View Solution
