Let us consider the situation when the axes are inclined at an angle ω . If the coordinates of a point P are (x1,y1), then PN=x1,PM=y1 where PM is parallel to the y-axis and PN is parallel to the Xaxis. The straight line through P that makes an angle θ with the x-axisis RQ=y−y1,PQ=x−x1 From ΔPQR, we have PQsin(ωθ)=√QRsinθory−y1=sinθsin(ω−θ)(x−x1) writen in the form of y−y1=m(x−x1) where m=sinθsin(ω−θ) Therefore, if the slope of the line is m, then the angle of inclination of the line with the x-axis is given by an tanθ=(msinω1+mcosω)
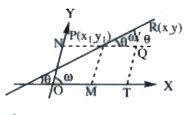
The axes being inclined at an angle of 60∘, the inclination of the straight line y=2x+5 with the x-axis is Solution in Telugu
30∘
tan−1(3/2)
tan−12
60∘
The correct Answer is:B
Step by step video, text & image solution for Let us consider the situation when the axes are inclined at an angle omega . If the coordinates of a point P are (x_1,y_1), then PN = x_1, PM =y_1 where PM is parallel to the y-axis and PN is parallel to the Xaxis. The straight line through P that makes an angle theta with the x-axisis RQ = y-y_1, PQ = x - x_1 " From " DeltaPQR, we have (PQ)/(sin(omega theta))=(sqrtQR)/(sin theta) or y-y_1 = (sin theta)/(sin(omega-theta))(x-x_1) writen in the form of y-y_1=m(x-x_1) " where " m=(sin theta)/(sin(omega-theta)) Therefore, if the slope of the line is m, then the angle of inclination of the line with the x-axis is given by an tan theta=((m sin omega)/(1+m cos omega)) The axes being inclined at an angle of 60^(@), the inclination of the straight line y=2x+5 with the x-axis is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - LECTURE SHEET(EXERCISE-I Problems on slopes, Equation of line intercepts of a lines, Areas)( Integer Type Question)5videos
STRAIGHT LINES
- BOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - LECTURE SHEET(EXERCISE-II Problems on form, symmetric form, Perpendicular distance and Ratio) ( Straight Objective Type Question)1videos
STRAIGHT LINES
- BOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - LECTURE SHEET(EXERCISE-I Problems on slopes, Equation of line intercepts of a lines, Areas)(Linked comprehension Type Question)1videos
STRAIGHT LINES
- BOOK - AAKASH SERIESCHAPTER - REVISION EXERCISEEXERCISE - PROPERTIES OF TRIANGLES57videos
REVISION EXERCISE
- BOOK - AAKASH SERIESCHAPTER - TANGENT AND NORMAL EXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS48videos
TANGENT AND NORMAL
Similar Questions
A and B are two fixed points such that AB=3 unit. P is a point such that PAPB=2 then the maximum area of triangle PAB is (in sq.units)
05:17View SolutionThe Incentre of a triangle formed by the line xcos(π9)=ysin(π9)=π,xcos(8π9)+ysin(8π9)=π,xcos(13π9)+ysin(13π9)=π is
03:54View SolutionA ray of light travelling along the line x+y = 1 line incident on the x-axis and after rrefraction it enters the other side of the x-axis by turing π/6 away from the x-axis. The equation of the line along which the refracted ray travels is
01:49View SolutionIn a triangle ABC, if A,B, C are in A.P and b:c =√3:√2, then
05:09View SolutionFind the equations of tangent and normal to the curve
(xa)4+(yb)4=2 at (a,b)03:24View SolutionThree points A(x1,y1),B(x2,y2)andC(x,y) are collinear. Prove that: (x−x1)(y2−y1)=(x2−x1)(y−y1).
01:48View SolutionProve that the line through the point x1,y1) and parallel to the line Ax+By+C=0 is A(x−x1)+B(y−y1)=0.
16:45View SolutionP(x1,y1),Q(x2,y2)బిందువులు గుండా పోయే సరళ రేఖ ధనాత్మ X-అక్షంతో θకోణం చేయుచున్న ఆ రేఖ వాలు.....
View SolutionProw that the line through the point (x1,y1)and parallel to the line Ax+By+C=0is A(x−x1)+B(y−y1)=0.
03:00View SolutionThe straight line passing through P(x1,y1) and making an angle α with x-axis intersects Ax+By+C=0 in Q then PQ =________________
02:17View SolutionProve that the line through the point (x1,y1) and parallel to the line Ax+By+C=0 is A(x−x1)+B(y−y1)=0.
02:45View SolutionLet us consider the situation when the axes are inclined at an angle ω . If the coordinates of a point P are (x1,y1), then PN=x1,PM=y1 where PM is parallel to the y-axis and PN is parallel to the Xaxis. The straight line through P that makes an angle θ with the x-axisis RQ=y−y1,PQ=x−x1 From ΔPQR, we have PQsin(ω−θ)=√QRsinθory−y1=sinθsin(ω−θ)(x−x1) writen in the form of y−y1=m(x−x1) where m=sinθsin(ω−θ) Therefore, if the slope of the line is m, then the angle of inclination of the line with the x-axis is given by an tanθ=(msinω1+mcosω)
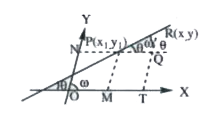
The axes being inclined at an angle of 60∘, the angle between the two straight line y=2x+5 and 2y+x+7=004:09View SolutionLet us consider the situation when the axes are inclined at an angle ω . If the coordinates of a point P are (x1,y1), then PN=x1,PM=y1 where PM is parallel to the y-axis and PN is parallel to the Xaxis. The straight line through P that makes an angle θ with the x-axisis RQ=y−y1,PQ=x−x1 From ΔPQR, we have PQsin(ω−θ)=√QRsinθory−y1=sinθsin(ω−θ)(x−x1) writen in the form of y−y1=m(x−x1) where m=sinθsin(ω−θ) Therefore, if the slope of the line is m, then the angle of inclination of the line with the x-axis is given by an tanθ=(msinω1+mcosω)

The axes being inclined at an angle of 30∘, the equation of the straight line which makes an angle of 60∘ with the positive directon of the x-axis and x-intercept 2 is04:44View SolutionFind the distance between P (x1,y1) and Q (x2,y2) when : (i) PQ is parallel to the y-axis, (ii) PQ is parallel to the x-axis.
03:57View SolutionProve that the line through the point (x1,y1) and parallel to the line Ax+By+C=0 is A(x−x1)+B(y−y1)=0.
01:41View Solution

