OPQR is square ('O' being origin and M,N are middle points of sides PQ, QR respectively and the ratio of areas of square and triangle OMN is pq(where P,q are relatively prime ) then P-q is Solution in Telugu
The correct Answer is:5
Step by step video, text & image solution for OPQR is square ('O' being origin and M,N are middle points of sides PQ, QR respectively and the ratio of areas of square and triangle OMN is p/q(where P,q are relatively prime ) then P-q is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - LECTURE SHEET(EXERCISE-II Problems on form, symmetric form, Perpendicular distance and Ratio) ( Straight Objective Type Question)1videos
STRAIGHT LINES
- BOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - LECTURE SHEET(EXERCISE-II Problems on form, symmetric form, Perpendicular distance and Ratio)( Straight Objective Type Question)31videos
STRAIGHT LINES
- BOOK - AAKASH SERIESCHAPTER - STRAIGHT LINESEXERCISE - LECTURE SHEET(EXERCISE-I Problems on slopes, Equation of line intercepts of a lines, Areas)(More than one correct answer Type Question)16videos
STRAIGHT LINES
- BOOK - AAKASH SERIESCHAPTER - REVISION EXERCISEEXERCISE - PROPERTIES OF TRIANGLES57videos
REVISION EXERCISE
- BOOK - AAKASH SERIESCHAPTER - TANGENT AND NORMAL EXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS48videos
TANGENT AND NORMAL
Similar Questions
The Incentre of a triangle formed by the line xcos(π9)=ysin(π9)=π,xcos(8π9)+ysin(8π9)=π,xcos(13π9)+ysin(13π9)=π is
03:01View SolutionA square of side "a" lies above the x-axis and has one vertex at the origin. The side passing through the origin makes an angle α where o<α<π4 with the positive direction of x-axis, the equation of its diagonal not passing through the origin is
03:43View SolutionThe coordinates of the points A and B are respectively (-3,2) and (2,3). P and Q are points on the line joining A and B such that AP=PQ. A square PQRS is constructed on PQ as one side, the coordinates of R can be
01:31View SolutionIn a triangle ABC, if A,B, C are in A.P and b:c =√3:√2, then
02:05View SolutionFind the equations of tangent and normal to the curve
(xa)4+(yb)4=2 at (a,b)03:30View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
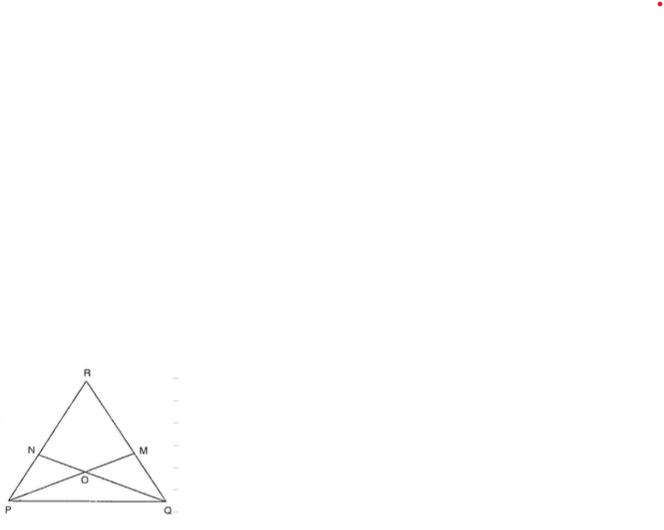 01:38View Solution
01:38View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
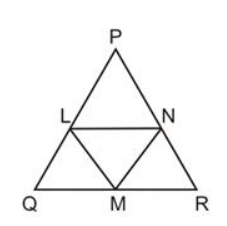 05:43View Solution
05:43View SolutionOPQR is a square and M,N are the middle points of the sides PQandQR , respectively. Then the ratio of the area of the square to that of triangle OMN is 4:1 (b) 2:1 (c) 8:3 (d) 7:3
03:18View SolutionOPQR is a square and M,N are the midpoints of the sides PQ and QR , respectively. If the ratio of the area of the square to that of triangle OMN is λ:6, then λ4 is equal to 2 (b) 4 (c) 2 (d) 16
04:12View SolutionIf p,q in N and 0,12=(p)/(q) where p and q are relatively prime then identify which of the following is incorrect
03:10View SolutionOPQR is a square and M,N are the middle points of the sides PQandQR , respectively. Then the ratio of the area of the square to that of triangle OMN is (a) 8:1 (b) 2:1 (c) 8:3 (d) 7:3
07:06View SolutionOPQR is a square and M,N are the midpoints of the sides PQ and QR , respectively. If the ratio of the area of the square to that of triangle OMN is λ:6, then λ4 is equal to 2 (b) 4 (c) 2 (d) 16
02:50View SolutionOPQR is a square and M,N are the middle points of the sides PQandQR , respectively. Then the ratio of the area of the square to that of triangle OMN is 4:1 (b) 2:1 (c) 8:3 (d) 7:3
04:44View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
04:00View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
04:43View Solution

