Match the following from List - I to List - II
List - IList - III.[1110](a)0II.[1111](b)1III.[0000](c)2IV.⎡⎢⎣100010001⎤⎥⎦(d)3
a,b,c,d
b,c,a,d
d,a,b,c
c,b,a,d
The correct Answer is:D
Topper's Solved these Questions
- MATRICES BOOK - AAKASH SERIESCHAPTER - MATRICES EXERCISE - LINEAR EQUATIONS - PRACTICE EXERCISE
15 Videos
- MATRICES BOOK - AAKASH SERIESCHAPTER - MATRICES EXERCISE - LINEAR EQUATIONS - EXERCISE - I
24 Videos
- MATHEMATICAL INDUCTIONBOOK - AAKASH SERIESCHAPTER - MATHEMATICAL INDUCTIONEXERCISE - PRACTICE SHEET (EXERCISE-I) LEVEL-I (Principle of Mathematical Induction) (Straight Objective Type Questions)
55 Videos
- MAXIMA & MINIMABOOK - AAKASH SERIESCHAPTER - MAXIMA & MINIMAEXERCISE - EXERCISE-III
35 Videos
Similar Questions
The truth table for the following combination of gates is
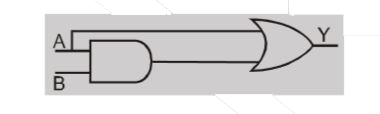
(a) ABY000010101111
(b) ABY000010100111
(c) ABY001011101110
(d) ABY0000111011110
View SolutionIf A=⎡⎢⎣011001000⎤⎥⎦ is a matrix of order 3 then the value of the matrix (I+A)−2A2(I−A), where I is a unity matrix is equal to (A) ⎡⎢⎣100110111⎤⎥⎦ (B) ⎡⎢⎣1−1−101−1001⎤⎥⎦ (C) ⎡⎢⎣11−1011001⎤⎥⎦ (D) ⎡⎢⎣002000000⎤⎥⎦
View Solution
Knowledge Check
Match the following :
List-IList-IIP251.0.70Q342.0.25R7103.0.40S144.0.75AP-4,Q-3,R-2,S-1BP-3,Q-4,R-1,S-2CP-1,Q-2,R-3,S-4DP-3,Q-1,R-4,S-2Which of the following sets of vectors in R3 are linearly independent ?
I [(1,0,0) , (0,1,0) ,(1,1,0)]
II [(1,0,0) , (0,1,0) ,(0,0,1)]
III [(0,1,0) , (1,0,1) ,(1,1,0)]
Iv [(0,0,1) , (0,1,0) ,(0,1,1)]
Select the correct answer using the codes given below.AI and IIBII and IIICIII and IVDI and IVIfA=[0−110] and B=[0iI0], then
AA2=IBA2=−ACB2=−IDB2=1
Find AB and BA if exists from the following matrices A and B:
(i)A=[23−1012]andB=[2−6−40]
(ii) A=⎡⎢⎣12301−2−10−1⎤⎥⎦andB=⎡⎢⎣002200020⎤⎥⎦
(iii)A=⎡⎢⎣03421−21−3−1⎤⎥⎦andB=[213−10−2]
View SolutionFind AB and BA if exists from the following matrices A and B:
(i)A=[23−1012]andB=[2−6−40]
(ii) A=⎡⎢⎣12301−2−10−1⎤⎥⎦andB=⎡⎢⎣002200020⎤⎥⎦
(iii)A=⎡⎢⎣03421−21−3−1⎤⎥⎦andB=[213−10−2]
View SolutionIf A=[i00i], n∈N , then A4n equals [0ii0] (b) [0000] (c) [1001] (d) [0ii0]
View SolutionIf A=⎡⎢⎣a000b000c⎤⎥⎦ and a,b,c are non zero real numbers, then A−1 is (A) 1abc⎡⎢⎣100010001⎤⎥⎦ (B) 1abc⎡⎢⎣a000b00c0⎤⎥⎦ (C) 1abc⎡⎢⎣a−1000b−100c−11⎤⎥⎦ (D) ⎡⎢⎣a−1000b−1000c−1⎤⎥⎦
View SolutionA=⎡⎢⎣1000110−24⎤⎥⎦,I=⎡⎢⎣100010001⎤⎥⎦
A−1=16(A2+CA+DI) then C and D equal to
View Solution
