मानाy की बढ़ती हुई धातों में (1+2y)10 के प्रसार में yr−1 का गुणांक k_(r) है। यदि kr+2kr=4 है, तो r का मान ज्ञात कीजिये।
The correct Answer is:5
Step by step video, text & image solution for मानाy की बढ़ती हुई धातों में (1+2y)^(10) के प्रसार में y^(r-1) का गुणांक k_(r) है। यदि (k_(r+2))/(k_(r)) =4 है, तो r का मान ज्ञात कीजिये। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- BINOMIAL THEOREM BOOK - BANSAL HINDICHAPTER - BINOMIAL THEOREM EXERCISE - EXERCISE - 3 (SECTION - A) (JEE - ADVANCED PREVIOUS YEARS.S QUESTIONS)
5 Videos
- BINOMIAL THEOREM BOOK - BANSAL HINDICHAPTER - BINOMIAL THEOREM EXERCISE - EXERCISE - 3 (SECTION - B) (JEE - ADVANCED PREVIOUS YEARS.S QUESTIONS)
11 Videos
- BINOMIAL THEOREM BOOK - BANSAL HINDICHAPTER - BINOMIAL THEOREM EXERCISE - EXERCISE - I SPECIAL DPP (SPECIAL DPP - 4)
18 Videos
- BASIC MATHEMATICS BOOK - BANSAL HINDICHAPTER - BASIC MATHEMATICS EXERCISE - EXERCISE -5 (Rank Booster)
9 Videos
- COMPLEX NUMBERBOOK - BANSAL HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE-5 (RANK BOOSTER)
13 Videos
Similar Questions
r=0,1,......10 के लिए, माना Ar,Br तथा Cr क्रमश: प्रदर्शित करते है (1+x)10,(1+x)20तथा (1+x)30 के प्रसार में xr के गुणांक को 1 तब 10∑r=1Ar(B10Br−C10Ar)बराबर है
View Solutionn∑r−0(r+1)nCr=(n+2)n−1
n∑r=0(r+1)nCrxr=(1+x)n+nx(1+x)n−1
View Solutionयदि 31.20C0+322.20C1+......21 पदों तक 2a−1b तो (ba) का मान होगा--
View Solutionमाना की A व्यक्त होगा समीकरण 15−4log4x+41+log4x=3 के मूलो के योग से, B व्यक्त होगा m व n के गुणनफल से जहाँ 2m=3 व 3n=4 , C व्यक्त होगा समीकरण log3x(3x)+(log3x)2=1 के पूर्णांक मूलो के योगफल से
A+B का मान होगा।
View Solutionदर्शाइये की गुणनफल, [1+(1+i2)][1+(1+i2)2][1+(1+i2)22].......[1+(1+i2)2n] का मान (1−122n)(1+i) के बराबर है, जहाँ n≥2 है।
View Solutionआकृति में O वृत्त का केंद्र है। यदि ∠APB=70∘ तो ∠AQB का मान है -
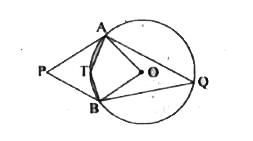
View Solutionसिद्ध कीजिए की (1−4x)1/2 के प्रसार में xr का गुणांक
⌊2r⌊r⌊r है|
View Solutionनिम्न व्यंजक के प्रसार में xn का गुणांक ज्ञात कीजिए|
1−x(1−x)3
View Solution1−2x+3x2ex के प्रसार में x5 का गुणांक ज्ञात कीजिए|
View Solutionमाना की α,β समीकरण px2+qx+r=0,p≠0 के मूल है | यदि p,q,r समान्तर श्रेणी में हों तथा 1α+1β=4 तो | α−β | का मात्र है :
View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
View Solution(1−t61−t)3 के प्रसार में t4 का गुणांक है
View Solutionयदि (1+xlog2x)5 के द्विपद प्रसार में तीसरा पद 2560 के बराबर है, तो x का एक सम्भव मान है
View Solution(1+x)2n के प्रसार में महत्तम गुणांक है
View Solutionयदि .8Cr−.7C3=.7C2, तब r का मान है
View Solutionआकृति में आपको दो वृत्त क्रमशः C(O, r) और C(O' r) दिए गए हैं| यदि उनकी संगत जीवाओं की लम्बाइयों में 1:1 का अनुपात हो तो उनके संगत केंद्रों में अंतरिक कोणों का अनुपात ज्ञात कीजिए |
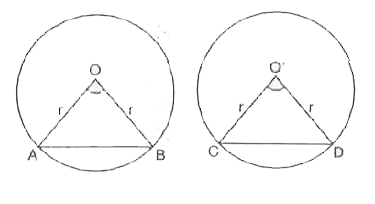
View Solution
