(i) यदि f(θ)=6∑n=1cosec(θ+(n−1)π4)cosec(θ+nπ4), जहाँ 0<θ<π2, तो f(θ) का न्यूनतम मान ज्ञात कीजिए |
(ii) माना fn(θ)=n∑n=1tan(θ2n)sec(θ2n−1) हो, तो f4(4π3) का मान ज्ञात कीजिए |
The correct Answer is:(i) 2√2, (ii) 2(√3−1)
Topper's Solved these Questions
- COMPOUND ANGLE (TRIGONOMETRY PHASE - I) BOOK - BANSAL HINDICHAPTER - COMPOUND ANGLE (TRIGONOMETRY PHASE - I) EXERCISE - EXERCISE -3 SECTION-A (JEE-ADVANCED PREVIOUS YEAR.S QUESTIONS)
9 Videos
- COMPOUND ANGLE (TRIGONOMETRY PHASE - I) BOOK - BANSAL HINDICHAPTER - COMPOUND ANGLE (TRIGONOMETRY PHASE - I) EXERCISE - EXERCISE -3 SECTION-B (JEE-MAIN PREVIOUS YEAR.S QUESTIONS)
4 Videos
- COMPOUND ANGLE (TRIGONOMETRY PHASE - I) BOOK - BANSAL HINDICHAPTER - COMPOUND ANGLE (TRIGONOMETRY PHASE - I) EXERCISE - EXERCISE -1 SPECIAL DPP-6
10 Videos
- COMPLEX NUMBERBOOK - BANSAL HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE-5 (RANK BOOSTER)
13 Videos
- CONIC SECTION (PARABOLA,ELLIPSE & HYPERBOLA)BOOK - BANSAL HINDICHAPTER - CONIC SECTION (PARABOLA,ELLIPSE & HYPERBOLA)EXERCISE - EXERCISE - 5
18 Videos
Similar Questions
इकाई त्रिज्या के तीन सिक्के (coins) एक समबाहु त्रिभुज में इस प्रकार से रखे जाते है कि वे परस्पर एक दूसरे को तथा त्रिभुज की भुजाओं को स्पर्श करते है तो त्रिभुज का क्षेत्रफल होगा
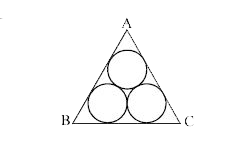
View Solutionकिसी ΔPQR में,यदि 3sinP+4cosQ=6 और 4sinQ+3cosP=1 तो ∠R बराबर है|
View Solutionव्यंजक 8∑θ=011+tan3(10θ)∘ का मान है : (i) 5 (ii) 214 (iii) 143 (iv) 92
View Solutionदर्शाइये की गुणनफल, [1+(1+i2)][1+(1+i2)2][1+(1+i2)22].......[1+(1+i2)2n] का मान (1−122n)(1+i) के बराबर है, जहाँ n≥2 है।
View Solutionबिन्दु P(h, k) से परवलय x2=8y पर तीन अभिलम्ब डाले गये है तथा m1,m2 तथा m3 इन तीनों की प्रवणताऐं है। इन तीनों अभिलम्बों की प्रवणताओं का बीजगणितीय योग ज्ञात कीजिए।
View SolutionIf |2sinθ−cosecθ|≥1andthη≠nπ2,n∈Z, then cos2θ≥12 (b) cos2θ≥14 cos2θ≤12 (d) cos2θ≤14
View Solutionfor 0
View Solutionf_(n)(theta)=sum_(n=1)^(n)tan((theta)/(2^(n)))sec((theta)/(2^(n-1))), then compute the value of f_(4)((4 pi)/(3))
View SolutionIf f(θ)=6∑n=1cosec(θ+(n−1)π4)cosec(θ+nπ4), where 0<θ<π2, then find the minimum value of f(θ).
View SolutionIf |2sinθ−cosecθ|≥1 and θ≠nπ2,n∈Z, then
View SolutionIf θ∈(π/4,π/2) and ∞∑n=11tannθ=sinθ+cosθ, then the value of tan θ is
View SolutionIf tan(πcotθ)=cot(πtanθ), then show that tanθ=14[2n+1±√4n2+4n−15], where n>1orn<−2.
View Solutionएक धन पूर्णांक n के लिए माना
fn(θ)=(tan.θ2)(1+secθ)(1+sec2θ)(1+sec4θ)...(1+sec2nθ), तब
View SolutionIf |2sinθ−cosecθ|≥1 and θ≠nπ2,n∈Z, then
View SolutionIf θ∈(π/4,π/2) and ∞∑n=11tannθ=sinθ+cosθ, then the value of tan θ is
View Solution
