z (वास्तविक या काल्पनिक) के उन मानों की संख्या जो कि समीकरणों 1+z+z2+z3+..........+z17=0और 1+z+z2+z3+.......+z13=0 को एक साथ सन्तुष्ट करती है, होगी
1
2
3
4
The correct Answer is:D
Step by step video, text & image solution for z (वास्तविक या काल्पनिक) के उन मानों की संख्या जो कि समीकरणों 1+z+z^2 +z^3+..........+z^17 = 0और 1+z+z^2+z^3+.......+z^13 = 0 को एक साथ सन्तुष्ट करती है, होगी by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - BANSAL HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE-1 (SPECIAL DPP-3)13videos
COMPLEX NUMBER
- BOOK - BANSAL HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE-1 (SPECIAL DPP-4)19videos
COMPLEX NUMBER
- BOOK - BANSAL HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE-5 (RANK BOOSTER)13videos
COMPLEX NUMBER
- BOOK - BANSAL HINDICHAPTER - BINOMIAL THEOREM EXERCISE - EXERCISE - 5 (RANK BOOSTER)12videos
BINOMIAL THEOREM
- BOOK - BANSAL HINDICHAPTER - COMPOUND ANGLE (TRIGONOMETRY PHASE - I) EXERCISE - EXERCISE - 5 (RANK BOOSTER)10videos
COMPOUND ANGLE (TRIGONOMETRY PHASE - I)
Similar Questions
चित्र में सम्मिश्र समतल में कुछ संख्याऐं दर्शायी गयी है तथा वृत्त एक इकाई वृत्त है जिसका केन्द्र मूल बिन्दु है, तब निम्न में से कौनसा एक F का प्रतिलोम होगा
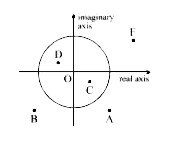 05:33View Solution
05:33View Solutionयदि z1 व z2 दो अशून्य (non - zero) सम्मिश्र संख्याएँ इस प्रकार है कि |z1+z2|=|z1|+|z2|, तब कोणांक (z1) - कोणांक (z2) का मान होगा
05:08View Solutionदर्शाइये की गुणनफल, [1+(1+i2)][1+(1+i2)2][1+(1+i2)22].......[1+(1+i2)2n] का मान (1−122n)(1+i) के बराबर है, जहाँ n≥2 है।
06:37View Solutionश्रेणी में (1+x)2012+(1+x2)2011+(1+x3)2010 असमान पदों की संख्या ज्ञात कीजिए।
05:43View Solutionमाना cosπ7+cos2π7−2 cos3π7 का यथार्थ मान एक परिमेय संख्या है जो कि pq के रूप में है, जहाँ p तथा q पूर्णांक है | (p + q) का मान ज्ञात कीजिए |
06:52View SolutionNumber of values of z (real or complex) simultaneously satisfying the system of equations 1+z+z2+z3++z17=0 and 1+z+z2+z3++z13=0 is
03:59View SolutionThe number of values of z (real or complex) e simultaneously satisfying the system of equations 1+z+z2+z3+...z17=0and1+z+z2+z3+..+z13=0 is
06:52View SolutionIf ={z:(1+2i)bar(z)+(1-2i)z+2=0) and B={z:(3+2i)+(3-2i)z+3=0, then
02:32View Solutionयदि किसी समबाहु त्रिभुज के शीर्ष z1,z2,z3 हो ताकि |z1|=|z2|=|z3| तो साबित करे z1+z2+z3=0
06:07View Solutionयदि z2+z+1=0, जहाँ z एक सम्मिश्र संख्या है तब
(z+1z)2+(z2+1z2)2+(z3+1z3)2+...+(z6+1z6)2 का मान होगा -04:13View Solutionसम्मिश्र संख्याओं z कि संख्या जो इस प्रकार |z−1|=|z+1|=|z−i|है, है :
07:04View Solutionयदि z2+z+1=0 जहाँ z एक सम्मिश्र संख्या है, तो (z+1z)2+(z2+1z2)2+(z3+1z3)2+......(z6+1z6)2 का मान है -
05:26View SolutionIf z^(2)+z+1=0 , where z is a complex number, then the value of (z+(1)/(z))^(2)+(z^(2)+(1)/(z^(2)))^(2)+(z^(3)+(1)/(z^(3)))^(2)+....+(z^(6)+(1)/(z^(6)))^(2) is
05:15View SolutionIf z^(2)+z+1=0 , where z is a complex number, then the value of (z+(1)/(z))^(2)+(z^(2)+(1)/(z^2))^(2)+(z^(3)+(1)/(z^3))^(2)+"……"+(z^(6)+(1)/(z^6))^(2) is
04:25View SolutionX(वास्तविक या सम्मिश्र) के मानों की संख्या जो समीकरण निकाय 1+z+z2+z3+……….+z17=0 तथा 1+z+z2+z3+…………+z13=0 को एक साथ संतुष्ट करते है होगी:
02:55View Solution

