एक कण का त्वरण [2ˆi+6tˆj+2π29cosπt3ˆk]ms−2 द्वारा दिया जाता है। t= 0 पर, →r=0 तथा →v=(2ˆi+ˆi)ms−1 है। t= 2 s पर स्थिति सदिश है
(8ˆi+10ˆj+ˆk)m
(8ˆi+10ˆj+3ˆk)m
(3ˆi+8ˆj+10ˆk)m
(10ˆi+3ˆj+8ˆk)m
The correct Answer is:B
Topper's Solved these Questions
- KINEMATICSBOOK - BANSAL HINDICHAPTER - KINEMATICSEXERCISE - EXERCISE - 1 (OBJECTIVE QUESTIONS) [PARAGRAPH TYPE]
11 Videos
- KINEMATICSBOOK - BANSAL HINDICHAPTER - KINEMATICSEXERCISE - EXERCISE - 1 (OBJECTIVE QUESTIONS) [REASONING TYPE]
9 Videos
- KINEMATICSBOOK - BANSAL HINDICHAPTER - KINEMATICSEXERCISE - EXERCISE - 5 (POTENTIAL PROBLEMS BASED ON CBSE)
17 Videos
- GRAVITATIONBOOK - BANSAL HINDICHAPTER - GRAVITATIONEXERCISE - EXERCISE-4 (IIT JEE Advanced Previous Year.s Questions)
14 Videos
- LAWS OF MOTIONBOOK - BANSAL HINDICHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - 5 ( Potential Problems Based on CBSE )
16 Videos
Similar Questions
सरल रेखा में गति करते हुए कण का वेग-समय वक्र चित्रानुसार है।
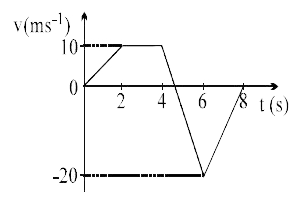
असत्य कथन का चयन करे। कण स्थिरावस्था में कब आएगा।
View Solutionकथन-1: सरल रेखीय गति में धनात्मक त्वरण का तात्पर्य यह नहीं होता है कि वस्तु की चाल बढ़ रही होगी।
कथन-2: त्वरण एवं वेग दोनों सदिश राशियां है।
View Solutionवह शर्त व्यक्त कीजिए जब गति में एक वस्तु (a) बिन्दु वस्तु के रूप में मानी जा सकती है (b) बिन्दु वस्तु के रूप में नहीं मानी जा सकती है।
View SolutionmA तथा mB द्रव्यमान के एक द्वि-तारा मण्डल में दो तारे वृत्ताकार पथ में घूम रहे है। यदि mA तथा mB द्रव्यमान के आवर्तकाल क्रमशः TA तथा TB हो, तो त्रिज्या तथा तथा द्रव्यमान mA तथा mB है तो
View Solutionएक आदर्श स्प्रिंग से 1kg की वस्तु लटकाने पर इसकी लम्बाई में 0.1 cm की वृद्धि हो जाती है। यदि यह स्प्रिंग एक घर्षणहीन क्षैतिज टेबल पर रखी जाये तथा इसके सिरों से प्रत्येक 1 kg की वस्तु लटकायी जाये, तो इसकी लम्बाई में वृद्धि क्या होगी?
View SolutionIf →a=ˆi+ˆj+ˆk&→b=ˆi−2ˆj+ˆi , then the vector →c such that →a.→c=2&→ax→c=→b is 13(ˆi−2ˆj+ˆk) (b) 13(−ˆi+2ˆj+5ˆk) 13(ˆi+2ˆj−5ˆk) (d) 12(−ˆi+2ˆj−5ˆk)
View SolutionIf →a=ˆi+ˆj+ˆk=ˆi−2ˆj+ˆk and the vector →c such that →a.→c=2 and →ax→c=→b then →c is 13(ˆi−2→j+→k) (2) 13(−ˆi+2ˆj+5ˆk) 13(ˆi+2ˆj−5ˆk) (4) 13(−ˆi+2ˆj−5ˆk)
View SolutionLet →A(t)=f1(t)ˆi+f2(t)ˆjand→B(t)=g(t)ˆi+g2(t)ˆj,t∈[0,1],f1,f2,g1g2 are continuous functions. If →A(t)and→B(t) are non-zero vectors for all tand→A(0)=2ˆi+3ˆj,→A(1)=6ˆi+2ˆj,→B(0)=3ˆi+2ˆiand→B(1)=2ˆj+6ˆj Then,show that →A(t)and→B(t) are parallel for some t.
View Solutionlet vec p-2hat i-hat j+hat k,vec k=hat i+2hat j-hat k and vec r=hat i+hat j-2hat k if vec V=vec p+lambdavec q and projection of vec V on vec r is (4)/(sqrt(5)) then lambda is
View SolutionIf vec a=2hat i+2hat j+3hat k,vec b=-hat i+2hat j+hat k and vec c=3hat i+hat j then vec a+tvec b is perpendicular to vec c if t=
View SolutionThe acceleration of a particle is given by vec(a) = [2hat(i)+6that(j)+(2pi^(2))/(9) "cos" (pit)/3hat(k)]ms^(-2) At t=0 ,vec(r)=0 and vec(v) =(2hat(i)+hat(j))ms^(-1) The position vector at t=2 s is
View SolutionThe vectors →a=(2−x)ˆi+2ˆj+2ˆk, →b=2ˆi+(2−y)ˆj+2ˆk, →c=2ˆi+2ˆj+(2−z)ˆkand→d=ˆi+ˆj+ˆk are coplanar, then
View Solutionउस समतल का सदिश समीकरण ज्ञात कीजिये जो बिन्दुओ ˆi−ˆk और 3ˆi+2ˆj+2ˆk से होकर गुजरता है तथा सदिश ˆi−2ˆj+3ˆk के समांतर है
View SolutionThe lines →r=ˆi+t(5ˆi+2ˆj+ˆk) and →r=ˆi+s(−10ˆi−4ˆj−2ˆk) are -
View SolutionFind the shortest distance between the following pairs of parallel lines whose equations are :
→r=(ˆi+ˆj)+t'(2ˆi−ˆj+ˆk) and →r=(2ˆi+ˆj−ˆk)+s'(4ˆi−2ˆj+2ˆk)
View SolutionFind the acute angle between the following lines.
→r=(4ˆi−ˆj)+t(ˆi+2ˆj−2ˆk)
→r=(ˆi−2ˆj+4ˆk)+s(−ˆi−2ˆj+2ˆk)
View Solution
