Expansion of ideal gas takes place from 1 L to 10 L in vacuum isothermally at 300 K. Which of the following is correct?
ΔH=0
q=0
w=0
All of these
To solve the problem regarding the isothermal expansion of an ideal gas from 1 L to 10 L at a temperature of 300 K, we can follow these steps:
Step 1: Understand the Process
The expansion of an ideal gas in vacuum is isothermal, meaning the temperature remains constant throughout the process. Since it is an ideal gas expanding in a vacuum, there is no external pressure opposing the expansion.
Step 2: Analyze the Change in Internal Energy (ΔU)
For an ideal gas undergoing an isothermal process, the change in internal energy (ΔU) is given by the equation:
ΔU=nCvΔT
Since the process is isothermal, ΔT = 0, which means:
ΔU=0
Step 3: Analyze the Change in Enthalpy (ΔH)
The change in enthalpy (ΔH) for an ideal gas is also dependent on temperature:
ΔH=nCpΔT
Again, since the temperature is constant (ΔT = 0), we have:
ΔH=0
Step 4: Work Done (W)
In an isothermal expansion in vacuum, the work done (W) is calculated using the formula:
W=−∫VfViPdV
However, since the gas is expanding in vacuum, the external pressure (P) is zero. Therefore:
W=0
Step 5: Heat Transfer (Q)
For an isothermal process, the heat transfer (Q) can be determined using the first law of thermodynamics:
ΔU=Q−W
Since ΔU = 0 and W = 0, we find:
0=Q−0⟹Q=0
Conclusion
In this isothermal expansion of an ideal gas in vacuum:
- ΔU = 0
- ΔH = 0
- W = 0
- Q = 0
Therefore, the correct answer to the question is that during the isothermal expansion in vacuum, the change in enthalpy (ΔH) is zero.
The expansion of an ideal gas in vacuum is isothermal, meaning the temperature remains constant throughout the process. Since it is an ideal gas expanding in a vacuum, there is no external pressure opposing the expansion.
For an ideal gas undergoing an isothermal process, the change in internal energy (ΔU) is given by the equation:
ΔU=nCvΔT
Since the process is isothermal, ΔT = 0, which means:
ΔU=0
The change in enthalpy (ΔH) for an ideal gas is also dependent on temperature:
ΔH=nCpΔT
Again, since the temperature is constant (ΔT = 0), we have:
ΔH=0
In an isothermal expansion in vacuum, the work done (W) is calculated using the formula:
W=−∫VfViPdV
However, since the gas is expanding in vacuum, the external pressure (P) is zero. Therefore:
W=0
For an isothermal process, the heat transfer (Q) can be determined using the first law of thermodynamics:
ΔU=Q−W
Since ΔU = 0 and W = 0, we find:
0=Q−0⟹Q=0
In this isothermal expansion of an ideal gas in vacuum:
- ΔU = 0
- ΔH = 0
- W = 0
- Q = 0
Topper's Solved these Questions
Similar Questions
How much heat is absorbed and how much work is done in the expansion?2L of an ideal gas at a pressure of 10 atm expansion isothermally into a vacuum until its total volume is 10L.
View SolutionIn an isothermal expansion of one mole of an ideal gas against vacuum from 10 litre to 100 litre at 27∘C, the quantity of heat absorbed by the gas is
View Solution
Knowledge Check
The reversible expansion of an ideal gas under adiabatic and isothermal conditions is shown in the figure. Which of the following statement(s) is (are) correct?
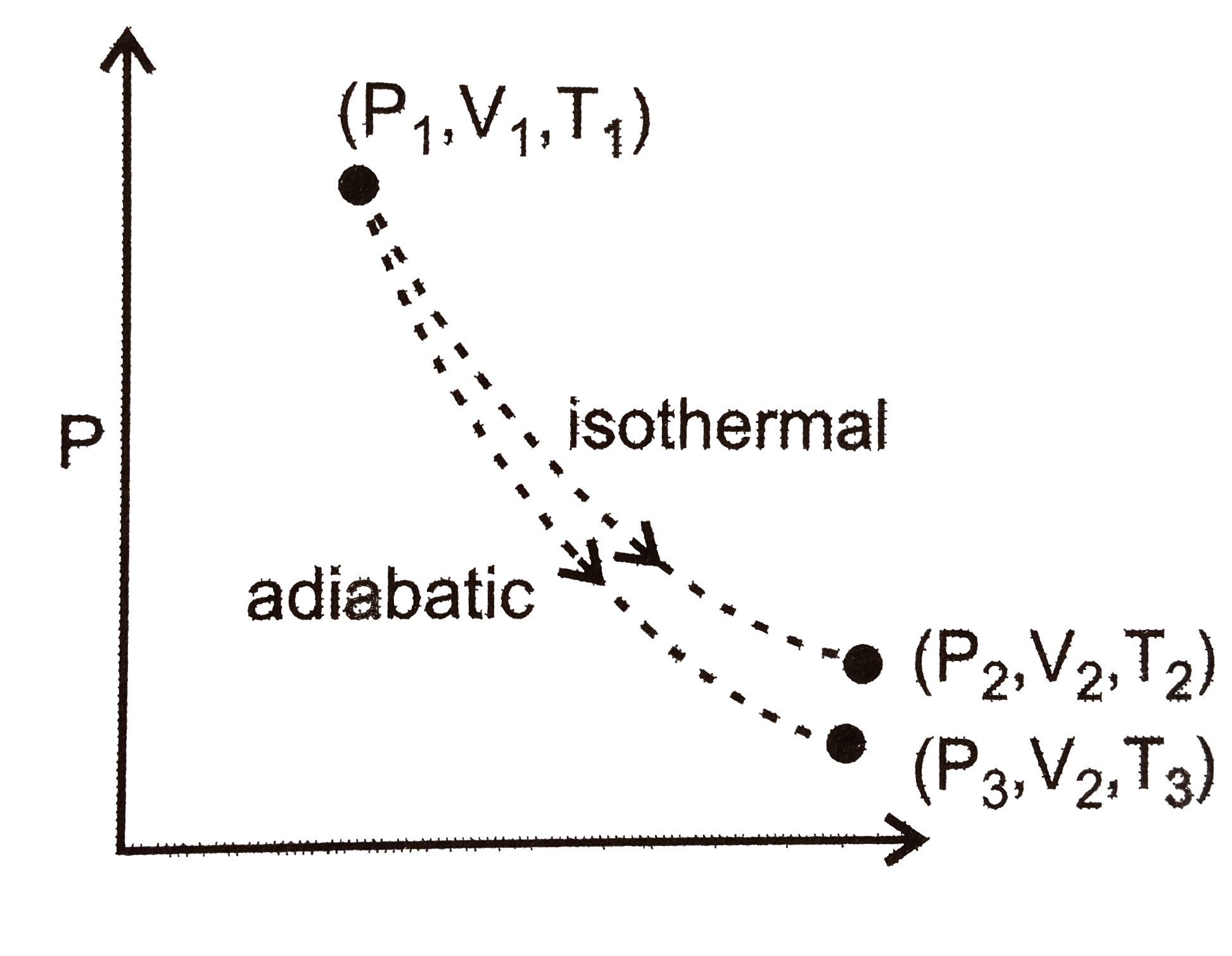 AT1=T2BT3>T1Cwisothermal>wadiabaticDΔUisothermal>ΔUadiabatic
AT1=T2BT3>T1Cwisothermal>wadiabaticDΔUisothermal>ΔUadiabaticWhat will the entropy change of the system when expansion of 1 mole of a gas takes place from 3 L to 6 L under isothermal conditions? Consider, R = 2 cal K−1 mol−1 and log 2 = 0.30
A2.84 cal K−1B1.386 cal K−1C0.37 cal K−1D5.26 cal K−12 mole of ideal gas expands isothermically and reversibally from 1 L to 10 L at 300 K. then ΔH is :
A4.98 kJB11.47 kJC−11.47kJDzero
In an isothermal expansion of one mole of an ideal gas against vacuum from 5 litre to 50 litre at 300 K, the quantity of heat absorbed by the gas is
View SolutionHeat obtained due to expansion of 1 mol of H2 gas at 1000 K from 10 L to 100L under isothermal reversible condition is absorbed by an engine having a sink at 300 K useful work obtained is
View Solution2 mol of an ideal gas expands isothermally and reversibly from 1 litre to 10 litres at 300 K. What is the enthalpy change?
View Solution4g of he gas is expanded isothermally at 300K from litre to 10L. The molar change in entropy is:
View Solution1 mole of an ideal gas undergoes an isothermal reversible expansion form 10 atm to 1 atm at 300 K. What will be the work done ?
View Solution
