A potentiometer circuit with potentiometer wire 10 m long, and an ideal main battery of e.m.f 8 V, has been set up for finding the internal resistance of a given cell. When the resistance R, connected across the given cell, has values of (i) infinity, (ii) 10 omega , the balancing lengths, on the potentiometer wire are found to be 2.4 m and x respectively. If the internal resistance of the cell is 2 omega, the value of x is
1m
6m
2m
8m
To find the value of x in the given potentiometer circuit, we can follow these steps:
Step 1: Understand the problem
We have a potentiometer circuit with a potentiometer wire of length 10 m and an ideal battery of e.m.f 8 V. The balancing lengths when the resistance R is infinite and 10 Ω are given as 2.4 m and x respectively. The internal resistance of the cell is given as 2 Ω.
Step 2: Use the potentiometer formula
The formula for the potentiometer in terms of balancing lengths and resistances is:
L1−L2L2=Rr
where:
- L1 is the balancing length for the infinite resistance (2.4 m),
- L2 is the balancing length for the resistance R (which is x),
- R is the external resistance (10 Ω),
- r is the internal resistance of the cell (2 Ω).
Step 3: Substitute the known values into the formula
Substituting the values into the formula, we have:
2.4−xx=102
This simplifies to:
2.4−xx=5
Step 4: Cross-multiply to solve for x
Cross-multiplying gives us:
2.4−x=5x
Step 5: Rearrange the equation
Rearranging the equation, we get:
2.4=5x+x
2.4=6x
Step 6: Solve for x
Now, divide both sides by 6:
x=2.46=0.4 m
Conclusion
The value of x is 0.4 m.
---
We have a potentiometer circuit with a potentiometer wire of length 10 m and an ideal battery of e.m.f 8 V. The balancing lengths when the resistance R is infinite and 10 Ω are given as 2.4 m and x respectively. The internal resistance of the cell is given as 2 Ω.
The formula for the potentiometer in terms of balancing lengths and resistances is:
L1−L2L2=Rr
where:
- L1 is the balancing length for the infinite resistance (2.4 m),
- L2 is the balancing length for the resistance R (which is x),
- R is the external resistance (10 Ω),
- r is the internal resistance of the cell (2 Ω).
Substituting the values into the formula, we have:
2.4−xx=102
This simplifies to:
2.4−xx=5
Cross-multiplying gives us:
2.4−x=5x
Rearranging the equation, we get:
2.4=5x+x
2.4=6x
Now, divide both sides by 6:
x=2.46=0.4 m
The value of x is 0.4 m.
Topper's Solved these Questions
Similar Questions
A potentiometer wire is 10 m long and has a resistance of 18Ω. It is connected to a battery of emf 5 V and internal resistance 2Ω. Calculate the potential gradient along the wire.
View SolutionWhen a balance point is obtained in a potentiometer for finding the internal resistance of a cell, the current through the potentiometer wire is due to
View Solution
Knowledge Check
A potentiometer circuit has been set up for finding the internal resistance of a given cell. The main battery, used across the potentiometer wire , has an emf of 2.0 v and a negligible internal resistance .The potentiometer wire itself is 4 m long . When the resistance , R connected across the given cell, has values of (i) Infinity , (ii) 9.5Ω the balancing length's on the potentiometer wire are found to be 3 m and 2.85 m , respectively . The value of internal resistance of the cell is .
A0.25ΩB0.95ΩC0.5ΩD0.75ΩA potentiometer circuit has been setup for finding. The internal resistance of a given cell. The main battery used a negligible internal resistance. The potentiometer wire itself is 4m long. When the resistance, R, connected across the given cell, has value of
(i) Infinity 9.5Ω,
(ii) the 'balancing length' , on the potentiometer wire are found to be 3m and 2.85m, respectively.
The value of internal resistance of the cell isA0.25ΩB0.95ΩC0.5ΩD0.75ΩIn an experiment to find the internal resistance of a cell by a potentiometer, a balance was obtained for 50 cm length of the potentiometer wire, with a cell of e.m.f. 2V. When the cell was shunted by a resistance of 2Ω, the balancing length of the potentiometer wire was 40 cm. What was the internal resistance of the cell ?
A0.25ΩB0.75ΩC0.5ΩD1Ω
If a ideal battery of e.m.f.10 V is connected with external resistance 9Ω and a wire of length 10 m and resistance 1Ω in series as shown in potentiometer wire

View SolutionA potentiometer wire , 4 m long and having a resistance of 10 Ω, is connected in series with an external resistance of 38Ω and a cell , of emf 2 V and internal resistance 2Ω. Calculate the potential gradient along the wire.
View SolutionA potentiometer wire, 4 m long and resistance 10Ω, is connected in series with a resistance of 1988 Ω and a cell of emf 2V and internal resistance 2Ω. What is the potential gradient along the wire?
View Solution3V poteniometer used for the determination of internal resistance of a 2.4V cell. The balanced point of the cell in open circuit is 75.8cm. When a resistor of 10.2Ω is used in the external circuit of the cell the balance point shifts to 68.3cm length of the potentiometer wire. The internal resistance of the cell is
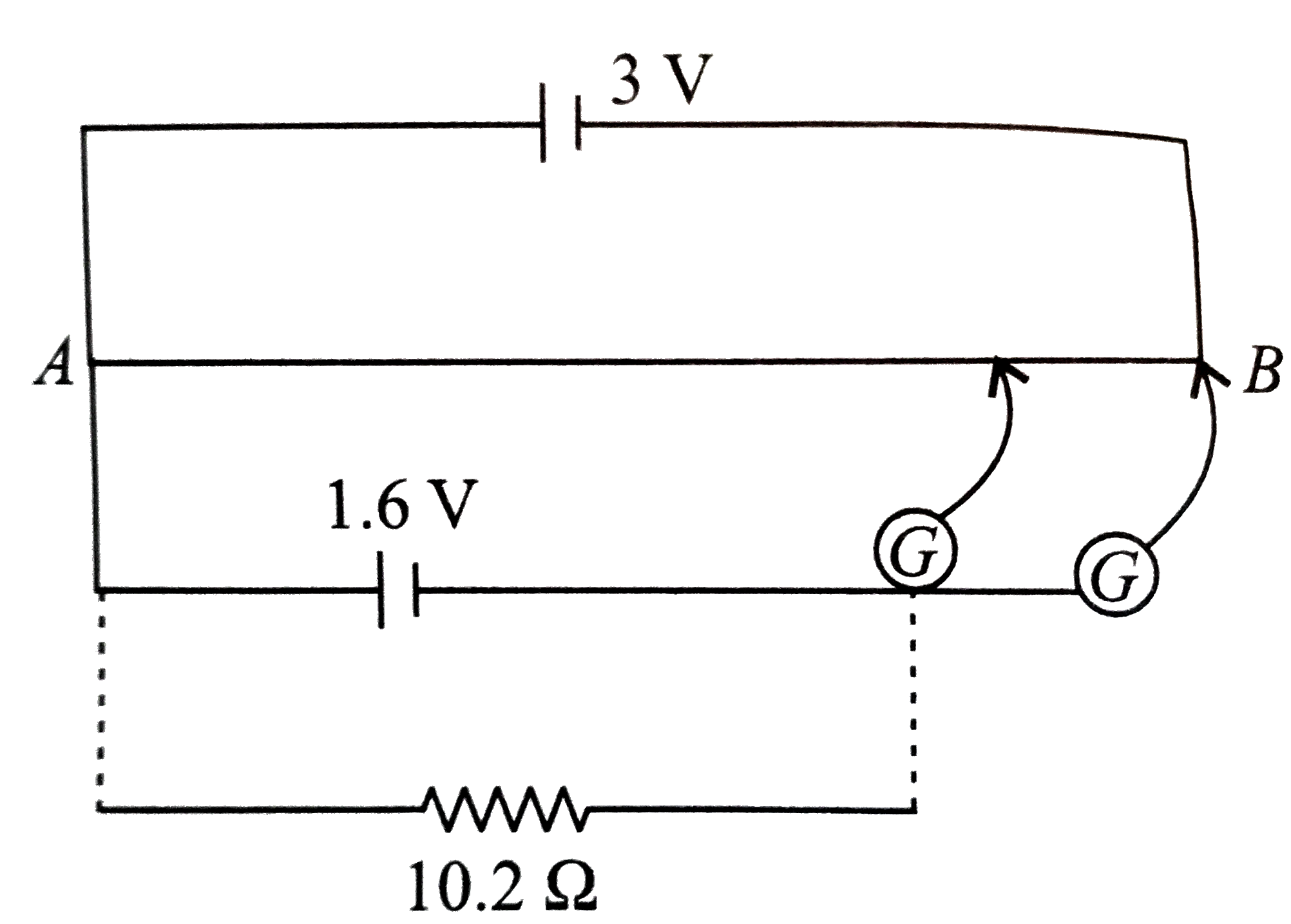
View SolutionThe wire of potentiometer has resistance 4Ω and length 1m. It is connected to a cell of e.m.f. 2V and internal resistance 1Ω. The current flowing through the potentiometer wire is
View Solution
