For a group of particles of different masses,if all the masses are placed at different points at equal distance R from the origin, then the distance of the centre of mass from the origin will be
More than R
Equal to R
At origin
Less than R
To find the distance of the center of mass from the origin for a group of particles of different masses placed at equal distances R from the origin, we can follow these steps:
Step 1: Understand the Configuration
We have a group of particles with different masses m1,m2,m3,…,mn placed at various points on a circle of radius R centered at the origin. The distance of each particle from the origin is the same, which is R.
Step 2: Write the Formula for Center of Mass
The formula for the center of mass →Rcm of a system of particles is given by:
→Rcm=∑mi→ri∑mi
where mi is the mass of the ith particle and →ri is the position vector of the ith particle.
Step 3: Analyze the Position Vectors
Since all particles are at the same distance R from the origin, we can express the position vectors →ri as:
→ri=R^ri
where ^ri is the unit vector in the direction of the position of the ith particle.
Step 4: Substitute into the Center of Mass Formula
Substituting →ri into the center of mass formula gives:
→Rcm=∑mi(R^ri)∑mi=R∑mi^ri∑mi
Step 5: Evaluate the Direction of the Center of Mass
The unit vectors ^ri point in different directions depending on the positions of the particles. If the particles are symmetrically distributed around the origin, the vector sum ∑mi^ri will equal zero because the contributions from opposite sides will cancel out.
Step 6: Conclusion
If the particles are not symmetrically distributed, the center of mass will still be at a distance R from the origin, but in a specific direction determined by the weighted average of the unit vectors. However, if we consider the average distance, it remains R.
Thus, the distance of the center of mass from the origin is:
Distance of center of mass from origin=R
Final Answer
The distance of the center of mass from the origin is R.
---
We have a group of particles with different masses m1,m2,m3,…,mn placed at various points on a circle of radius R centered at the origin. The distance of each particle from the origin is the same, which is R.
The formula for the center of mass →Rcm of a system of particles is given by:
Since all particles are at the same distance R from the origin, we can express the position vectors →ri as:
Substituting →ri into the center of mass formula gives:
The unit vectors ^ri point in different directions depending on the positions of the particles. If the particles are symmetrically distributed around the origin, the vector sum ∑mi^ri will equal zero because the contributions from opposite sides will cancel out.
If the particles are not symmetrically distributed, the center of mass will still be at a distance R from the origin, but in a specific direction determined by the weighted average of the unit vectors. However, if we consider the average distance, it remains R.
The distance of the center of mass from the origin is R.
Topper's Solved these Questions
Similar Questions
A large number of particles are placed around the origin, each at a distance R from the origin. The distance of the center of mass of the system from the origin is
View SolutionAll the particles of body are situated at a distance R from the origin. The distance of the centre of mass of the body from the origin is also R. Is this statement true or false?
View Solution
Knowledge Check
The distance of centre of mass from O is
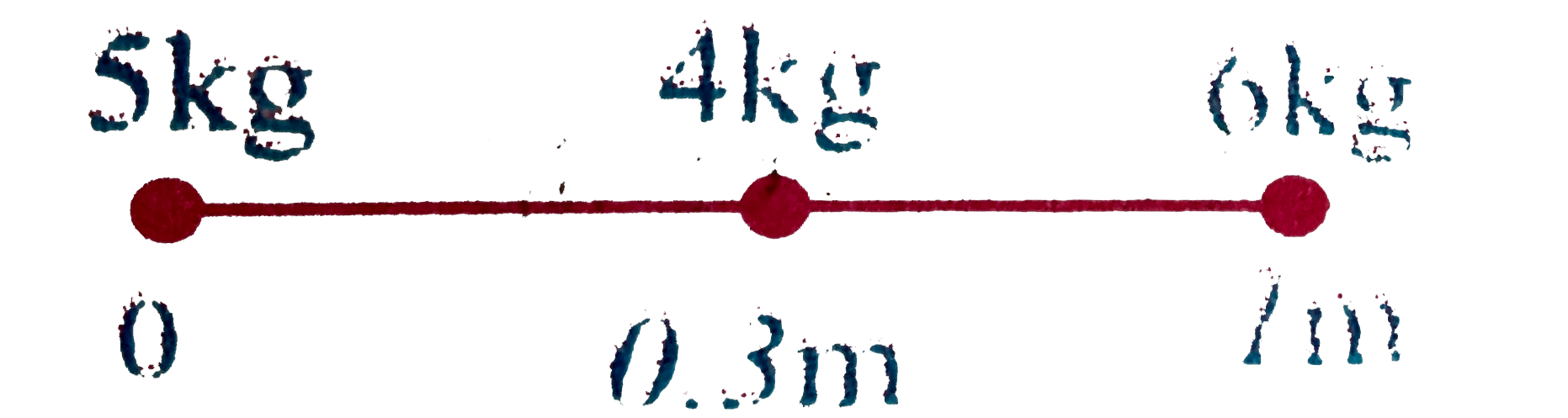 A0.21mB0.35mC0.42mD0.48m
A0.21mB0.35mC0.42mD0.48mAll the particles of a body are situated at a distance R from the origin. The distance of the centre of mass of the body from the origin is
A=RB≤RC>RD≥RAll the particles of a body situated at distance d from the origin. The distance of the center of mass of the body from the origin is
A=dB≤dC>dD≥d
A large number of particles are placed around the origin, each at a distance R from the origin. The distance of the center of mass of the system from the origin is
View SolutionThree masses are placed on the x-axis : 300 g at origin , 500 g at x = 40 cm and 400 g at x = 70 cm . The distance of the centre of mass from the origin is
View SolutionA circular hole of radius r is made in a disk of radius R and of uniform thickness at a distance a from the centre of the disk. The distance of the new centre of mass from the original centre of mass is
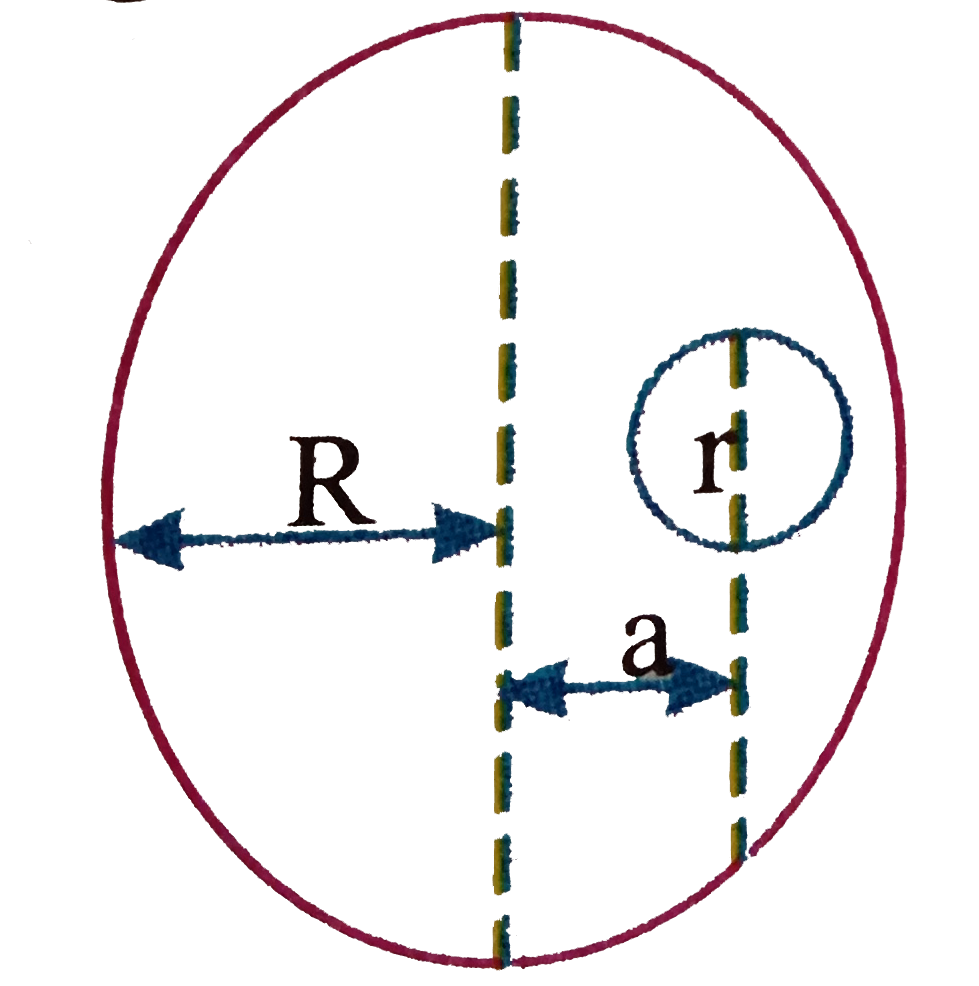
View SolutionThree masses are placed on the x-axis : 300g at origin. 500g at x=40cm and 400g at x=70cm. The distance of the centre of mass from the origin is.
View SolutionIf the distance between two point masses m1 and m2 is d, then distance of its centre of mass from m2 will be mod
View Solution