Starting from the surface of earth, the variation of acceleration due to gravity (g) with height (h) can be represented by
To solve the problem of how the acceleration due to gravity (g) varies with height (h) above the Earth's surface, we can follow these steps:
1. Understand the Formula for Gravity at the Surface of the Earth:
The acceleration due to gravity at the surface of the Earth is given by:
g=GMR2
where:
- G is the universal gravitational constant,
- M is the mass of the Earth,
- R is the radius of the Earth.
2. Determine the Formula for Gravity at Height h:
At a height h above the Earth's surface, the distance from the center of the Earth becomes R+h. The acceleration due to gravity at this height h is given by:
g′=GM(R+h)2
3. Relate g′ to g:
To express g′ in terms of g, we can write:
g′=GM(R+h)2=g⋅R2(R+h)2
Here, we substituted g=GMR2.
4. Simplify the Expression:
Therefore, we can express the variation of gravity with height as:
g′=g⋅R2(R+h)2
5. Final Expression:
This can be further simplified to:
g′=g⋅(1+hR)−2
This shows how the acceleration due to gravity decreases as we go higher above the Earth's surface.
Final Result:
The variation of acceleration due to gravity g′ with height h can be represented as:
g′=g⋅(1+hR)−2
The acceleration due to gravity at the surface of the Earth is given by:
g=GMR2
where:
- G is the universal gravitational constant,
- M is the mass of the Earth,
- R is the radius of the Earth.
At a height h above the Earth's surface, the distance from the center of the Earth becomes R+h. The acceleration due to gravity at this height h is given by:
g′=GM(R+h)2
To express g′ in terms of g, we can write:
g′=GM(R+h)2=g⋅R2(R+h)2
Here, we substituted g=GMR2.
Therefore, we can express the variation of gravity with height as:
g′=g⋅R2(R+h)2
This can be further simplified to:
g′=g⋅(1+hR)−2
This shows how the acceleration due to gravity decreases as we go higher above the Earth's surface.
The variation of acceleration due to gravity g′ with height h can be represented as:
g′=g⋅(1+hR)−2
Similar Questions
Draw graphs showing the variation of accleeration due to gravity with (a) height above the Earth's surface, (b) depth below the Earth's surface.
View SolutionWhich of the following graphs shows an approximate variation of acceleration due to gravity g with height h above the Earth's surface?

View Solution
Knowledge Check
Starting from the centre of the earth having radius R the variation of g (acceleration due to gravity) is shown by
A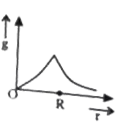 B
B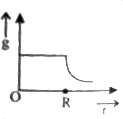 C
C D
D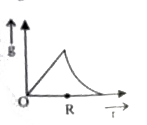
Starting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
A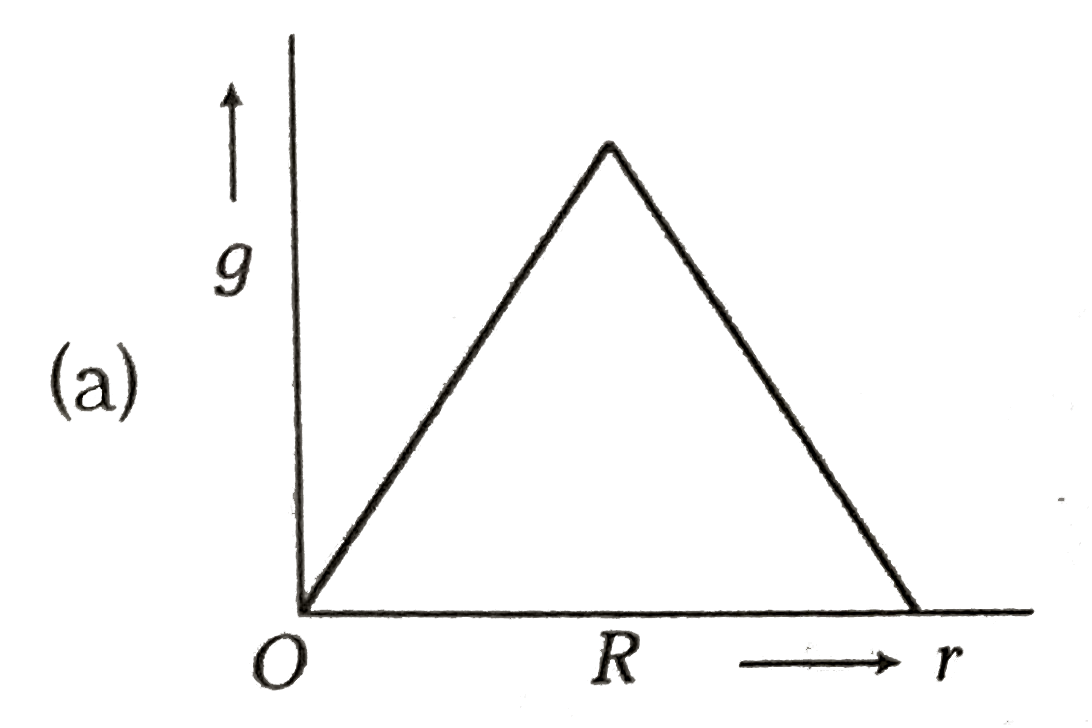 B
B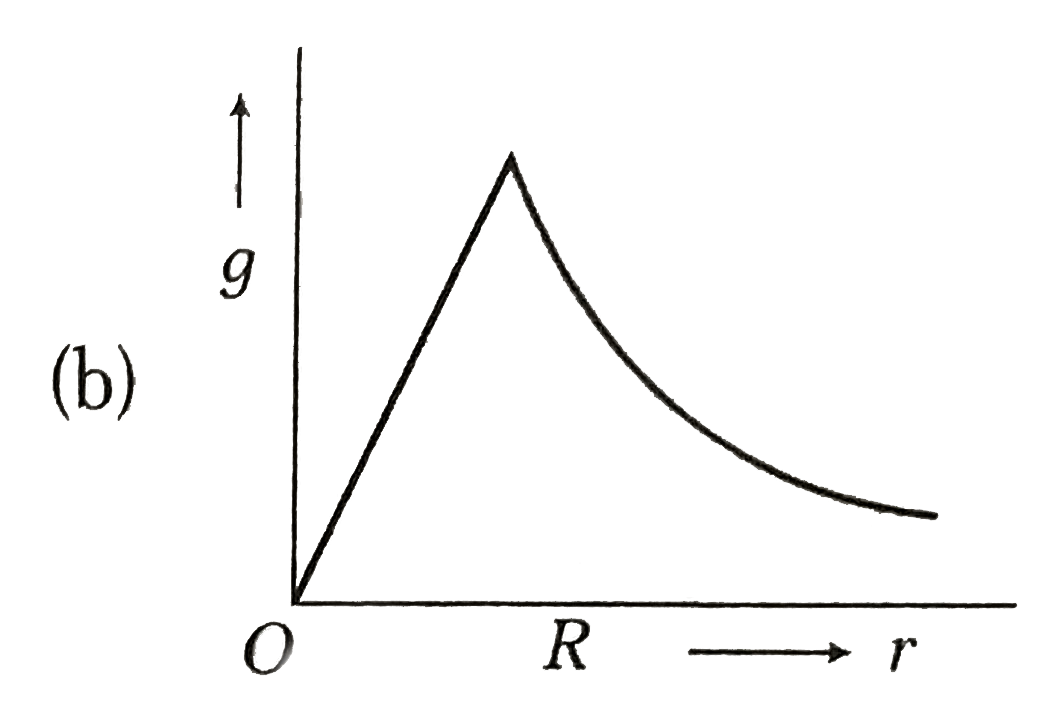 C
C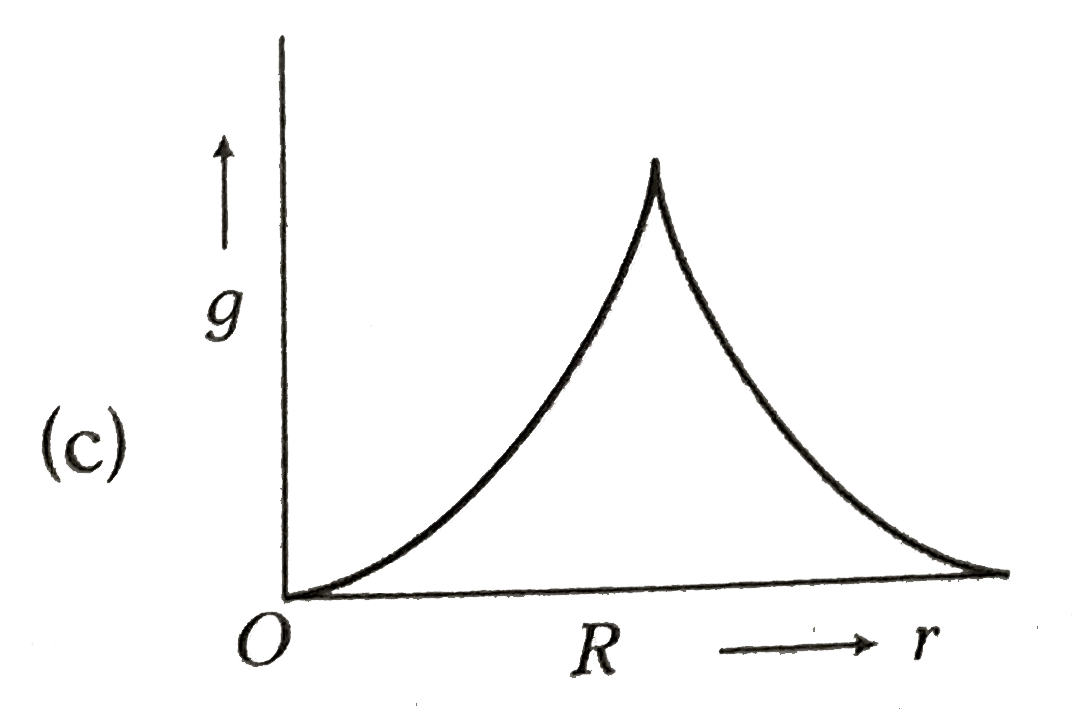 D
D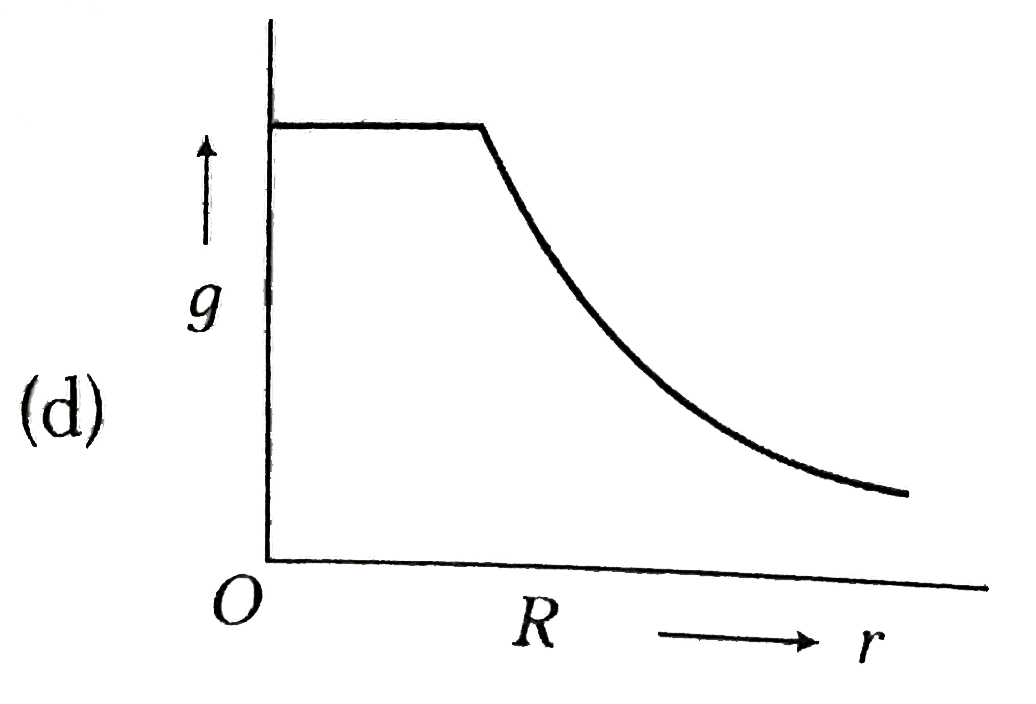
A body is taken to a height of nR from the surface of the earth . The ratio of acceleration due to gravity on the surface to that at the altitude is
A(n+1)2B(n+1)−2C(n+1)−1D(n+1)
Does the concentration of the earth's mass near its centre change the variation of g (acceleration due to gravity) with height from its surface?
View SolutionAt what depth from the surface of the earth, the acceleration due to gravity will be half the value of g on the surface of the earth ?
View SolutionThe value of the acceleration due to gravity g on earth depends upon
View SolutionAcceleration due to gravity is ‘ g ’ on the surface of the earth. The value of acceleration due to gravity at a height of 32 km above earth’s surface is (Radius of the earth = 6400 km )
View SolutionAt what distance from the centre of the earth, the value of acceleration due to gravity g will be half that on the surface ( R = radius of earth)
View Solution
