In series L−R circuit, XL=R. Now a capacitor with XC=R is added in series. New power factor
Same as initial
1√2 times the initial
12 times the initial
√2 times the initial
To solve the problem, we need to find the new power factor of a series L-R circuit when a capacitor is added in series. Let's break it down step by step.
Step 1: Understand the initial circuit
In the initial L-R circuit, we have:
- Inductive reactance XL=R
- Resistance R
Step 2: Calculate the impedance of the L-R circuit
The impedance Z of the L-R circuit can be calculated using the formula:
Z=√R2+X2L
Since XL=R, we can substitute:
Z=√R2+R2=√2R2=R√2
Step 3: Calculate the initial power factor
The power factor cosϕ is given by:
cosϕ=RZ
Substituting the value of Z:
cosϕ=RR√2=1√2
Step 4: Add the capacitor to the circuit
Now, a capacitor is added in series with XC=R. The new impedance Z′ of the L-R-C circuit is given by:
Z′=√(XL−XC)2+R2
Since XL=R and XC=R, we have:
Z′=√(R−R)2+R2=√0+R2=R
Step 5: Calculate the new power factor
The new power factor cosϕ′ is given by:
cosϕ′=RZ′
Substituting the value of Z′:
cosϕ′=RR=1
Conclusion
The new power factor after adding the capacitor in series is 1.
In the initial L-R circuit, we have:
- Inductive reactance XL=R
- Resistance R
The impedance Z of the L-R circuit can be calculated using the formula:
Z=√R2+X2L
Since XL=R, we can substitute:
Z=√R2+R2=√2R2=R√2
The power factor cosϕ is given by:
cosϕ=RZ
Substituting the value of Z:
cosϕ=RR√2=1√2
Now, a capacitor is added in series with XC=R. The new impedance Z′ of the L-R-C circuit is given by:
Z′=√(XL−XC)2+R2
Since XL=R and XC=R, we have:
Z′=√(R−R)2+R2=√0+R2=R
The new power factor cosϕ′ is given by:
cosϕ′=RZ′
Substituting the value of Z′:
cosϕ′=RR=1
The new power factor after adding the capacitor in series is 1.
Topper's Solved these Questions
Similar Questions
An ac circuit has an inductor and a resistor of resistance R in series, such that XL=3R.Now, a capacitor is added in series such that XC=2R. The ratio of new power factor with the old power factor of the circuit is √5:x. The value of x is_________
View SolutionIn series L-C-R circuit the quality factor is
View Solution
Knowledge Check
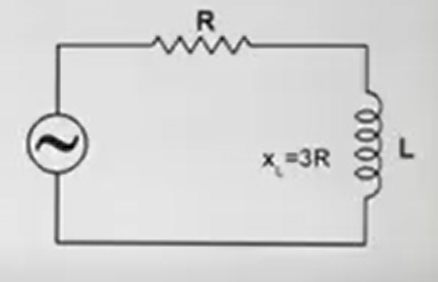
In series LR circuit, XL=3R. Now a capacitor with XC=R is added in series. The ratio of new to old power factor
A√2B1√2C2D1In L−C−R series circuit
Acurrent may achieve same value for two different value of frequencyBcurrent can not achieve same value for two different values of frequencyCcurrent is maximum for a maximum value of frequencyDnone of theseIn L−C−R series AC circuit,
AIf R is increased, then current will decreaseBIf L is increased, then current will decreaseCIf C is increased, then current will increaseDIf C is increased, then current will decrease
In series L-C-R circuit the quality factor is
View SolutionThe power factor of the circuit shown is p. Now a capacitor (Xc=2R) is also joined in series. Find p1p2
View Solution(i) An a.c. Source of voltage V=V0 sin ωt is connected to a series combination of L,C and R . Use the phasor diagram to obtain expression for impedance of the circuit and phase angle between voltage and current . Find the condition when current will be phase with the voltage . What is the circuit in this condition called ?
(ii) In a series LR circuit XL=R and power factor of the circuit is P1. When capacitor which capacitance C such that XL=XC is put in series , the power factor becomes P2 .Calculate P1/P2

View SolutionIn a series LR circuit XL=R and power factor of the circuit is P1 . When capacitor with capacitance C such that XL=XC is put in series, the power factor becomes P2 . Calculate P1P2
View SolutionIn a series resonant L-C-R circuit, the power factor is
View Solution
