Consider the function y=xx√x
Express the above function as logy=(x+12)logxSolution in Malayalam
Step by step video & image solution for Consider the function y=x^xsqrtx Express the above function as logy=(x+1/2)logx by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Consider the following figure
find the point of intersection (P) of the parabola and the line.
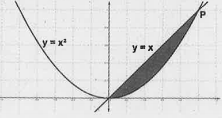 01:33View Solution
01:33View SolutionUsing properties of determinants prove
∣∣ ∣ ∣∣xyx+yyx+yxx+yxy∣∣ ∣ ∣∣=−2(x3+y3)05:42View Solutioniflogx - logy = 1 and x+y = 11 then x = ______
03:30View SolutionIf y=axax...∞, prove that dydx=y2(logy)x[1−y(logx)(logy)].
02:14View Solutionxdydx=y(logy−logx+1)
05:45View SolutionExpress xdydx=y(logy−logx+1) in the form F(yx)=dydx
05:19View Solutionxdydx=y(logy−logx−1)
02:45View SolutionIf log(x+y3)=12(logx+logy), then dydx=
03:23View SolutionIf xlogy=logx, prove that, xy.dydx=1−logxlogy(logx)2
01:23View SolutionIf y=xyx, prove that, dydx=ylogy(1+xlogxlogy)xlogx(1−xlogy).
08:22View Solutionlogx + logy = log(x+y) అయిన x=
03:13View SolutionSuppose x,y,z=0 and are not equal to 1 and logx+logy+logz=0. Find the value of 1xlogy+1^(logz)1ylogz+1^(logx)1zlogx+1^(logy)
04:50View Solutionxdydx=y(logy−logx+1)
03:35View SolutionIf y=axax...∞, prove that dydx=y2(logy)x[1−y(logx)(logy)]
03:14View SolutionThe solution of the differential equation dydx=x2+xy+y2x2, is
a.) tan−1(xy)=logy+C b.) tan−1(yx)=logx+C c.) tan−1(xy)=logx+C d.) tan−1(yx)=logy+C04:29View Solution

