If dydx=1dxdy , Show that d2ydx2=−d2xdy2(dxdy)3Solution in Malayalam
Step by step video & image solution for If dy/dx=1/(dx/dy) , Show that (d^2y)/(dx^2)=(-(d^2x)/dy^2)/((dx/dy)^3) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
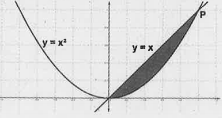
Consider the following figure
find the point of intersection (P) of the parabola and the line.
 08:53View Solution
08:53View SolutionUsing properties of determinants prove
∣∣ ∣ ∣∣xyx+yyx+yxx+yxy∣∣ ∣ ∣∣=−2(x3+y3)02:09View SolutionIf R=[1+(dydx)2]3/2d2ydx2 , thenR2/3 can be put in the form of 1(d2ydx2)2/3+1(d2xdy2)2/3 b. 1(d2ydx2)2/3−1(d2xdy2)2/3 c. 2(d2ydx2)2/3+2(d2xdy2)2/3 d. 1(d2ydx2)2/3.1(d2xdy2)2/3
01:41View SolutionFind the order and degree of (d2ydx2)3+(dydx)2+sin(dydx)+1=0
04:30View Solution(d2ydx2)2+d2ydx2−(dydx)4+dydx+y=6x3 অবকল সমীকরণের মাত্রা-
01:49View Solutionनिम्न अवकल समीकरण की कोटि तथा घात ज्ञात कीजिये :
(i)d2ydx2+dydx+y=ex (ii)dydx+√y+(dydx)=0
(iii)d2ydx2=5(dydx)32 (iv)dydx+y=sinx02:42View Solutiondxdy=u এd2xdy2=v হলে d2ydx2-এর মান কত হবে?
03:26View SolutionDifferential equation ((d^2y)/(dx^2))^3+((dy)/(dx))^2+sin(dy/(dx))+1=0 Is the power of
05:26View Solutiond2xdy2 equals: (1) (d2ydx2)−1 (2) −(d2ydx2)−1(dydx)−3 (3) −(d2ydx2)−1(dydx)−2 (4) −(d2ydx2)−1(dydx)3
04:12View Solutiond2xdy2 equals: (1) (d2ydx2)−1 (2) −(d2ydx2)−1(dydx)−3 (3) (d2ydx2)−1(dydx)−2 (4) −(d2ydx2)−1(dydx)−3
07:53View SolutionIf R=[1+(dydx)2]3/2d2ydx2 , thenR2/3 can be put in the form of a. 1(d2ydx2)2/3+1(d2xdy2)2/3 b. 1(d2ydx2)2/3−1(d2xdy2)2/3 c. 2(d2ydx2)2/3+2(d2xdy2)2/3 d. 1(d2ydx2)2/31(d2xdy2)2/3
02:24View SolutionIf R=[1+(dydx)2]−3/2d2ydx2 , thenR2/3 can be put in the form of 1(d2ydx2)2/3+1(d2xdy2)2/3 b. 1(d2ydx2)2/3−1(d2xdy2)2/3 c. 2(d2ydx2)2/3+2(d2xdy2)2/3 d. 1(d2ydx2)2/3.1(d2xdy2)2/3
03:08View SolutionIn dydx, x is independent variable and y is the dependent variable. If independent and dependent variables are interchanged dydx becomes dxdy and these two are connected by the relation dydx.dxdy=1 . Find a relation between d2ydx2 and d2xdy2
02:31View SolutionIn dydx,x is a independent variable and y is the dependent variable. If independent and dependent variables are interchanged dydx becomes dxdy and these two are connected by the relation dydx.dxdy=1 . Find a relation between d2ydx2andd2xdy2 .
02:20View Solutiond2xdy2 equals:
(1.) (d2ydx2)−1
(2) −(d2ydx2)(dydx)−3
(3) −(d2ydx2)−1(dydx)−2
(4) −(d2ydx2)−1(dydx)303:54View Solution

