The three urns having the numbers of white and black balls are given below :
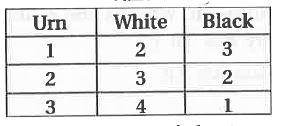
The probability of chosing every urn is equl. A ball is chosen randomly from the urn is found to be white. Then find the probability that the ball chosen was that form urn-2.Solution in Gujrati
The correct Answer is:
Step by step video, text & image solution for The three urns having the numbers of white and black balls are given below : The probability of chosing every urn is equl. A ball is chosen randomly from the urn is found to be white. Then find the probability that the ball chosen was that form urn-2. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Solutions of NCERT Exemplar Problems (Objective type Questions)38videos
PROBABILITY
- BOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Solutions of NCERT Exemplar Problems (True/False)10videos
PROBABILITY
- BOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Solutions of NCERT Exemplar Problems (Short Answer Type Questions)40videos
PROBABILITY
- BOOK - KUMAR PRAKASHANCHAPTER - MATRICES EXERCISE - Practice Paper - 3 (Section - D)1videos
MATRICES
- BOOK - KUMAR PRAKASHANCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Practice Paper - 1 (Section - D)2videos
RELATIONS AND FUNCTIONS
Similar Questions
If P(A)=45 and P(A∩B)=710 then P(B/A) is equal to = ……..
10:48View SolutionLet P(A)>0 and P(B)>0. Then, A and B can be both mutually exclusive and independent.
06:42View SolutionFor a loaded die, the probabilities of outcomes are given as under :
P(1)=P(2)=0.2,P(3)=P(5)=P(6)=0.1 and P(4)=0.3.
The die is thrown two times. Let A and B be the events, 'same number each time', and 'a total score is 10 or more', respectively. Determine whether or not A and B are independent.05:12View SolutionFor matrix A=⎡⎢⎣11112−32−13⎤⎥⎦ . Prove that , A3−6A2+5A+11I=0. Hence find A−1 using it .
02:02View SolutionLet : f:N→N be defined by f(n)={n+12 if n is oddn2 if n is even for all n∈N .
State whether the function f is bijective . Justify your answer.04:43View SolutionUrn A contains 2 white, 1 black and 3 red balls, urn B contains 3 white, 2 black and 4 red balls and urn C contains 4 white, 3 black and 2 red balls. One urn is chosen at random and 2 balls are drawn at random from the urn. If the chosen balls happen to be red and black, what is the probability that both balls come from urn B?
01:54View SolutionA die is rolled and showing any number is directly proportional to that number. If prime number appears then a ball is chosen from urn A containing 2 white and 3 black balls otherwise a ball is chosen from urn B containing 3 white and 2 black balls Then.
If white ball is draw then the probability that it is from urn B06:26View SolutionThere are three urns containing 2 white and 3 black balls, 3 white and 2 black balls and 4 white and 1 black balls, respectively. There is an equal probability of each urn being chosen. A ball is drawn at random from the chosen urn and it is found to be white. Find the probability that the ball drawn was from the second urn.
04:35View Solutionएक कलश में 8 लाल 6 सफ़ेद तथा 4 काली गेंदे है । कलश से यदृच्छया एक गेंद निकली जाती है । कलश से सफ़ेद गेंद निकालने कि प्रायिकता है :
View SolutionThree Urns have the following composition of balls.
Urn I : 1 white, 2 black
Urn II : 2 white, 1 black
III : 2 white, 2 black
One of the Urn is selected at random and a ball is drawn. It turns out to be white. Find the probability that it come from Urn III.04:31View Solutionएक कलश में 15 गेंद है। जिनमें में 5 सफेद और 10 काली गेंद है। कलश में से एक नीली गेंद निकालनी की प्रायिकता ज्ञात कीजिए।
05:30View SolutionThree identical urns contain white and black balls. The first urn contains 2 white and 3 black balls, the second urn 3 white and 2 black balls and the third urn 1 black and 4 white balls. An urn is chosen at random and a ball is drawn from it. If the ball drawn is white, what is the probability that the first urn is chosen ?
01:59View SolutionThere are 2 white , 4 black balls in urn A, In urn B, there are 5 white and 7 black balls. If one ball is randomly replaced from A and B , and a ball is drawn from B then the probability for the ball to be white one is
View SolutionAn urn contains 8 white and 5 black balls while another urn contains 5 white and 6 black balls.One urn is chosen at random and two balls are drawn from it. Find the probability that the balls are white.
05:50View SolutionSuppose there are 3 urns containing 2 white, 3 black balls, 4 white 1 black and 3 white, 2 black balls respectively. There is equal chance for selecting an urn. One ball is drawn from an urn chosen at random and it is found to be white. The prob. That it was drawn from the first urn is
06:53View Solution

