सिद्ध करो : nPr=n−1Pr+r.n−1Pr−1
Step by step video & image solution for सिद्ध करो : ""^(n)P_(r) = ""^(n-1)P_(r) +r .""^(n-1) P_(r-1) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- क्रमचय एवं संचय BOOK - BANSAL HINDICHAPTER - क्रमचय एवं संचय EXERCISE - EXERCISE-3 ( SECTION-A (JEE-ADVANCED PREVIOUS YEAR.S QUESTIONS))
16 Videos
- क्रमचय एवं संचय BOOK - BANSAL HINDICHAPTER - क्रमचय एवं संचय EXERCISE - EXERCISE-3 ( SECTION-B (JEE-MAIN PREVIOUS YEAR.S QUESTIONS))
13 Videos
- क्रमचय एवं संचय BOOK - BANSAL HINDICHAPTER - क्रमचय एवं संचय EXERCISE - EXERCISE-1(SPECIAL DPP)( SPECIAL DPP-10)
15 Videos
- अवकल समीकरण एवं व्रक से घिरा क्षेत्रफल BOOK - BANSAL HINDICHAPTER - अवकल समीकरण एवं व्रक से घिरा क्षेत्रफल EXERCISE - Exercise -5 (Rank Booster)
12 Videos
- फलन की सीमा सत्त्यता तथा अवकलनीयता BOOK - BANSAL HINDICHAPTER - फलन की सीमा सत्त्यता तथा अवकलनीयता EXERCISE - Exercise -5 (Rank Booster)
5 Videos
Similar Questions
शब्द ENDEANOEL के अक्षरों के सभी सम्भावित क्रमचय लीजिये।
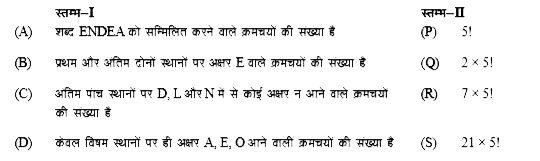
View Solutionशब्द MISSISSIPPI के अक्षरों से बनाये जाने वाले विभिन्न शब्दों की संख्या, जिनमें दो S एक साथ नहीं हो, होगी।
View Solutionएक अलमारी में 100 विभिन्न किताबें है तो उनमें से तीन किताबे कितनी तरह से चुनी जा सकती है जबकि कोई भी दो किताबे पास-पास की न हो
View Solutionसभी फलन f(x) ज्ञात कीजिए, जो वास्तविक मान के साथ (−π2,π2) पर परिभाषित हो तथा जिसका पूर्वग F(x) इस प्रकार है कि f(x)+cosx.F(x)=sin2x(1+sinx)2 है।
View Solutionयदि l=Limn→∞n∑r=2((r+1)sinπr+1−rsinπr) है, तो {l} मान ज्ञात करो। (जहाँ पर {} भिन्नात्मक भाग फलन है)
View SolutionProve that .n−1Pr+r.n−1Pr−1=.nPr
View SolutionProve that:
(i) nPn=nPn−1 (ii) nPr=n⋅n−1Pr−1 (iii) n−1Pr+r⋅n−1Pr−1=nPr
View Solutionसिद्ध कीजिए कि-
(i) nPr=(n−r+1).nPr−1 , (ii) nPr=n−1Pr+r,n−1Pr−1
(iii) nPrnPr−2=(n−r+2)(n−r+1)
(iv) 2npn=2n[1.3.5....(2n−1)]
View Solutionसिद्ध कीजिए कि -
(i) nPn=nPn−1 , (ii) nPr=rPn.nPn−r
View Solutionसिद्ध कीजिए कि nPr=n.n−1Pr−1
View Solutionसिद्ध कीजिए कि -
(i) .nPr.nPr−2=(n−r+1)(n−r+2)
(ii) .n−1Pr+r⋅.n−1Pr−1=.nPr
(iii).2nPn=2n⋅{1⋅3⋅5⋅…⋅(2n−1)}
View SolutionProve that .nPr=.n−1Pr+r.n−1Pr−1.
View SolutionShow that , .nPr=n.n−1Pr−1=(n−r+1).nPr−1.
View Solutionसिद्ध कीजिए कि:
.nPr=.n−1Pr+r(.n−1Pr−1)
View Solutionदर्शाइए कि: 1⌊r.nPr+1⌊(r−1).nPr−1=1⌊r.n+1Pr
View SolutionIf ""^(n)P_(r)=""^(n)P_((r+1)) and ""^(n)C_(r) = ""^(n)C_(r-1), then (n,r) =
View Solution
