माना λ1 तथा λ2,λ के ऐसे दो मान है जिनके लिए व्यंजक x2+(2−λ)x+λ−34 एक पूर्ण वर्ग बन जाता है, तो (λ21+λ22)का मान है
8
25
50
100
The correct Answer is:C
Step by step video, text & image solution for माना lambda_(1) तथा lambda_(2), lambda के ऐसे दो मान है जिनके लिए व्यंजक x^(2) + ( 2 - lambda) x + lambda - (3)/(4) एक पूर्ण वर्ग बन जाता है, तो (lambda_(1)^(2) + lambda_(2)^(2))का मान है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - BANSAL HINDICHAPTER - QUADRATIC EQUATIONEXERCISE - Exercise - 1 [Special Dpp 2 ]10videos
QUADRATIC EQUATION
- BOOK - BANSAL HINDICHAPTER - QUADRATIC EQUATIONEXERCISE - Exercise - 1 [Special Dpp 3]10videos
QUADRATIC EQUATION
- BOOK - BANSAL HINDICHAPTER - PROBABILITYEXERCISE - EXERCISE-5 (RANK BOOSTER)11videos
PROBABILITY
- BOOK - BANSAL HINDICHAPTER - RELATION & FUNCTION EXERCISE - EXERCISE - 5 (Rank Booster)16videos
RELATION & FUNCTION
Similar Questions
एक द्विघात बहुपद y=px2−qx+r का आरेख संलग्न चित्रानुसार है, तो
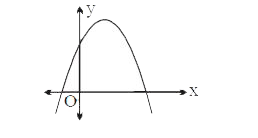 05:34View Solution
05:34View Solutionएक द्विघातीय त्रिपद P(x) इस प्रकार है कि P(x)=0 एवं P(P(Px)) = 0 का एक उभयनिष्ठ मूल है , तो
08:11View Solution4 स्वतन्त्र प्रयासों पर विचार कीजिए जिनमें एक एक घटना A के घटित होने की प्रायिकता 13 है। यदि घटना A कम से कम दो बार घटित होती है तो घटना B के घटित होने की प्रायिकता 1 है। यदि घटना A घटित नहीं हो तो घटना Bघटित नहीं हो सकती है। यदि घटना Aएक बार घटित होती है तो B की घटित होने की प्रायिकता 12है। यदि घटना B के घटित होने की प्रायिकता P को mn के रूप में व्यक्त किया जा सके, तो (m +n) का न्यूनतम मान ज्ञात कीजिये,जहाँ m, n∈ N है।
03:06View Solutionनिम्न फलनों के प्रान्त व परिसर ज्ञात कीजिये।
y=log√5(√2(sinx−cosx)+3)04:34View SolutionIf alpha,beta be the roots of the equation lambda^(2)(x^(2)-x)+2 lambda x+3=0 and lambda_(1),lambda_(2) be the two values of lambda for which alpha and beta are connected by the relation (alpha)/(beta)+(beta)/(alpha)=(4)/(3), then find the equation whose roots are ((lambda_(1))^(2))/(lambda_(2)) and ((lambda_(2))^(2))/(lambda_(1))
View SolutionIf lambda_(1),lambda_(2)(lambda_(1)>lambda_(2)) are two values of lambda for which the expression f(x,y)=x^(2)+lambda xy+y^(2)-5x-7y+6 can be resolved as a product of two linear factors, then the value of 3 lambda_(1)+2 lambda_(2) is
04:38View SolutionLet λ1,λ2 be two values of λ for which the expression x2+(2−λ)x+λ−34 becomes a perfect square. The value of (λ21+λ22) equals (i) 8 (ii) 25 (iii) 50 (iv) 100
06:09View SolutionTwo particle are moving perpendicular to each with de-Broglie wave length lambda_(1) and lambda_(2) . If they collide and stick then the de-Broglie wave length of system after collision is : (A) lambda = (lambda_(1) lambda_(2))/(sqrt(lambda_(1)^(2) + lambda_(2)^(2))) (B) lambda = (lambda_(1))/(sqrt(lambda_(1)^(2) + lambda_(2)^(2))) (C) lambda = (sqrt(lambda_(1)^(2) + lambda_(2)^(2)))/(lambda_(2)) (D) lambda = (lambda_(1) lambda_(2))/(sqrt(lambda_(1) + lambda_(2)))
View SolutionSolve the foregoing problem if lambda_(1)=lambda_(2)=lambda
07:25View SolutionIf α,β are the roots of the equation λ(x2−x)+x+5=0 and if λ1andλ2 are two values of λ obtained from αβ+βα=45, then λ1λ22+λ2λ21 equals
03:09View SolutionIf the matrix A=⎡⎢ ⎢⎣λ21λ1λ2λ1λ3λ2λ1λ22λ2λ3λ3λ1λ3λ2λ23⎤⎥ ⎥⎦ is idempotent,
the value of λ21+λ22+λ23 is04:30View SolutionLet αandβ be the values of x obtained form the equation λ2(x2−x)2λx+3=0andifλ1,λ2 be the two values of λ for which αandβ are connected by the relation αβ+βα=43 . then find the value of λ21λ2+λ21λ1andλ21λ22+λ22λ21
07:25View Solutionalpha , beta are the roots of the equation lambda (x^(2) - x) + x + 5 = 0 . If lambda_(1) and lambda_(2) are the two values of lambda for which the roots alpha , beta are connected by the relation (alpha)/(beta) + (beta)/(alpha) = 4. Then the value of (lambda_(1))/(lambda_(2)) + (lambda_(2))/(lambda_(1)) is :
05:10View SolutionTwo particle are moving perpendicular to each with de-Broglie wave length lambda_(1) and lambda_(2) . If they collide and stick then the de-Broglie wave length of system after collision is : (A) lambda = (lambda_(1) lambda_(2))/(sqrt(lambda_(1)^(2) + lambda_(2)^(2))) (B) lambda = (lambda_(1))/(sqrt(lambda_(1)^(2) + lambda_(2)^(2))) (C) lambda = (sqrt(lambda_(1)^(2) + lambda_(2)^(2)))/(lambda_(2)) (D) lambda = (lambda_(1) lambda_(2))/(sqrt(lambda_(1) + lambda_(2)))
View Solutionयदि α,β समीकरण λ(x2−x)+x+5=0 के मूल हैं तथा यदि λ1 व λ2,αβ+βα=45 से प्राप्त λ के दो मान हैं, तब λ1λ22+λ2λ21=?
09:11View Solution

