माना g:R→R एक फलन है जो g(x)={ex} द्वारा परिभाषित है जहाँ {x} भिन्नात्मक भाग फलन को दर्शाता है
कथन-1 g(x) आवर्ती फलन है
कथन-2 {x} आवर्ती फलन है
कथन 1 सत्य है कथन 2 सत्य है एवं कथन 2 कथन 1 का सही स्पष्टीकरण करता है
कथन 1 सत्य है कथन 2 सत्य है परन्तु कथन 2 कथन 1 का सही स्पष्टीकरण नहीं करता है
कथन 1 सत्य तथा कथन 2 असत्य है
कथन 1 असत्य तथा कथन 2 सत्य है
The correct Answer is:D
Step by step video, text & image solution for माना g:RtoR एक फलन है जो g(x)={e^(x)} द्वारा परिभाषित है जहाँ {x} भिन्नात्मक भाग फलन को दर्शाता है कथन-1 g(x) आवर्ती फलन है कथन-2 {x} आवर्ती फलन है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - BANSAL HINDICHAPTER - RELATION & FUNCTION EXERCISE - EXERCISE - 1 (SPECIAL DPP - 5 )9videos
RELATION & FUNCTION
- BOOK - BANSAL HINDICHAPTER - RELATION & FUNCTION EXERCISE - EXERCISE - 1 (SPECIAL DPP - 6)10videos
RELATION & FUNCTION
- BOOK - BANSAL HINDICHAPTER - RELATION & FUNCTION EXERCISE - EXERCISE - 1 (SPECIAL DPP - 3 )10videos
RELATION & FUNCTION
- BOOK - BANSAL HINDICHAPTER - QUADRATIC EQUATIONEXERCISE - Exercise - 5 (Rank Booster)11videos
QUADRATIC EQUATION
- BOOK - BANSAL HINDICHAPTER - SOLUTION OF TRIANGLE EXERCISE - EXERCISE - 5 (Rank Booster)5videos
SOLUTION OF TRIANGLE
Similar Questions
y=g(x) का आरेख दर्शाया गया है तो समीकरण के ||g(x)|−1|=12 के हलो की संख्या होगी -
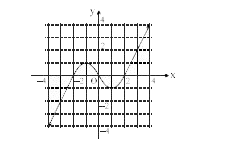 03:05View Solution
03:05View Solutionयदि समीकरण (p2−4)(p2−9)x3+[p−22](x2+p−4)+(p2−5p+6)x+{2p−1}=0 अन्तराल (0,x) के सभी मानों द्वारा संतुष्ट होती है, तो 'p' के सभी संभव पूर्णांक मानो का योगफल है
{y} तथा [y] क्रमशः y के भिन्नात्मक भाग फलन एवं महत्तम पूर्णांक फलन को निरूपित करते है ]00:53View Solutionमाना F(x)=⎡⎢ ⎢⎣x|x| यदि x≤−1[1+x]+[1−x] यदि −1<x<1−x|x| यदि x≥1
जहाँ [x] महत्तम पूर्णांक फलन है तो F(x) है01:45View Solutionएक द्विघात बहुपद f(x)=x2+ax+b इस प्रकार है कि इसका एक शून्य 4+3√32+√3 है, जहाँ a तथा b पूर्णांक है। साथ ही, g(x)=x4+2x3−10x2+4x−10 एक चतुर्थघातीय बहुपद इस प्रकार है कि g(4+3√32+√3)=c√3+d है, जहाँ c तथा d भी पूर्णांक है। a, b, c एवं d के मान ज्ञात कीजिये।
02:06View Solutionएक समकोणीय त्रिभुज ABC में ∠A=90∘ है माना M भुजा BC का मध्य - बिन्दु है यदि त्रिभुज ABM तथा त्रिभुज ACM के अन्तःवृत्त की त्रिज्याएँ क्रमशः r1 एवं r2 हो तो r1/r2 के मानों का परिसर ज्ञात कीजिए।
03:20View Solutionफलन f(x)=2sinx का आयाम है -
04:16View Solutionयदि फलन f(x) द्वारा अधिकतम मान x व y न्यूनतम मान ग्रहण किया जाता है तो इस फलन का आयाम . . . . . . . है ।
04:01View Solutionकोई फलन किसी बिन्दु x = a पर अवकलनीय कहलता है, जब -
03:47View Solutionयदि द्विअवकलनीय f(x) फलन x=a पर स्थानीय उच्चिष्ठ है , तो
06:01View Solutionवह अन्तराल ज्ञात कीजिए जिसमें फलन f(x)=x−2x+1 एक वर्धमान फलन है।
01:27View Solutionअन्तराल ज्ञात कीजिये जिनमे से निम्लिखित फलन वर्धमान है या हसयमन है। >br>f(x)=x4−2x2
01:43View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।04:50View Solutionफलन x2logx अन्तराल (1,e) में रखता है
01:45View Solutionफलन f(x)=In(π+x)In(e+x) है
05:23View Solutionयदि फलन f (x) आवर्त का सतत फलन है , तो समाकलन I=∫a+Taf(x)dx का मान है
02:52View Solutionअंतराल (0,π2) में फलन log sin x है
05:18View Solution

