एक न्यूनकोणीय त्रिभुज ABC में, शीर्ष A,B एवं C से विपरीत भुजा पर डाले गये लम्ब की लम्बाई क्रमशः AD,BE एवं CF है तो
[% प्रयुक्त किये गये सभी प्रतीकों का त्रिभुज में समान्य अर्थ है ]
ΔDEF की परित्रिज्या है
abc8Δ
a4sinA
R2
r6cosecA2cosecB2cosecC2
The correct Answer is:A, B, C, D
Topper's Solved these Questions
- SOLUTION OF TRIANGLE BOOK - BANSAL HINDICHAPTER - SOLUTION OF TRIANGLE EXERCISE - EXERCISE -2
21 Videos
- SOLUTION OF TRIANGLE BOOK - BANSAL HINDICHAPTER - SOLUTION OF TRIANGLE EXERCISE - EXERCISE -3 SECTION - A (JEE ADVANCED Previous Year.s Questions)
10 Videos
- SOLUTION OF TRIANGLE BOOK - BANSAL HINDICHAPTER - SOLUTION OF TRIANGLE EXERCISE - EXERCISE - 1 SPECIAL DPP -3
12 Videos
- RELATION & FUNCTION BOOK - BANSAL HINDICHAPTER - RELATION & FUNCTION EXERCISE - EXERCISE - 5 (Rank Booster)
16 Videos
- TRIGONOMETRIC EQUATIONS AND INEQUATIONSBOOK - BANSAL HINDICHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - EXERCISE - 5 (Rank Booster)
10 Videos
Similar Questions
सामान्य संकेतो का उपयोग करते हुए एक त्रिभुज ABC में निम्न को सिद्ध कीजिये।
r1(s−b)(s−c)+r2(s−c)(s−a)+r3(s−a)(s−b)=3r
View Solutionमाना ABC एवं ABC' दो त्रिभुज है जो सर्वागमस नहीं है एवं AB=4,AC=AC'=2√2 तथा कोण B=30∘ है इन दोनों त्रिभुजों के क्षेत्रफलों के अन्तरका निरपेक्ष मान ज्ञात कीजिये।
View Solutionमाना ABC एक समकोण त्रिभुज है तथा भुजा AB की लम्बाई 3 एवं विकर्ण AC की लम्बाई 5 है यदि D, BC पर एक बिन्दु इस प्रकार है कि BDDC=ABAC है तो AD का मान है
View Solutionनिम्न फलनों के प्रान्त व परिसर ज्ञात कीजिये।
y=log√5(√2(sinx−cosx)+3)
View Solutionत्रिकोणमितीय समीकरण 3(12+log3(cosx+sinx))−2log2(cosx−sinx)=√2 का व्यापक हल ज्ञात कीजिए।
View Solutionकिसी त्रिभुज के शीर्ष (0,0),(1,2) तथा (−3,3) है , तो शीर्षो से सम्मुख भुजाओ पर डाले गये लम्बो कि लम्बाई ज्ञात कीजिए
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionत्रिभुज ABC की मध्याकाओं की लम्बाई ज्ञात कीजिए, जिसके शीर्ष A(3, -2), B(0, 6) और C(-2, 4) है ।
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solutionदिये गये चित्र में स्पर्श रेखाओ की संख्या है -
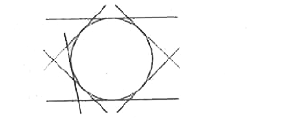
View Solutionदिये गये चित्र में स्पर्श रेखाओ की संख्या है:

View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionमाना एक दीर्घवृत्त कि नाभियां S तथा S' है तथा इसके लघु अक्ष का कोई एक शीर्ष B है। यदि ΔS'BS एक समकोण त्रिभुज है जिसका समकोण B पर है तथा ΔS'BS का क्षेत्रफल 8 वर्ग इकाई है, तो दीर्घवृत्त की एक नाभिलम्ब जीवा की लम्बाई है
View Solutionपरवलय y2=4ax की स्पर्श रेखा पर नाभि से डाले गये लम्ब के पाद का बिन्दुपथ है
View Solution
