What is sum of the interior angles of a regular polygon of n sides?Solution in Assamese
Step by step video & image solution for What is sum of the interior angles of a regular polygon of n sides? by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A Square and a rectanglar field with measurements as given in the figure have the same perimeter. Which filed has a larger area?
View SolutionFind the values of the letters in each of the following and give reasons for the steps involved.
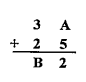
View SolutionThe interior angle of a n sided regular polygon is 48∘ more than the interior angle of a regular hexagon. Find n.
View SolutionIn an n-sided regular polygon, each exterior angle is 72∘. Find the sum of all the interior angles of the polygon.
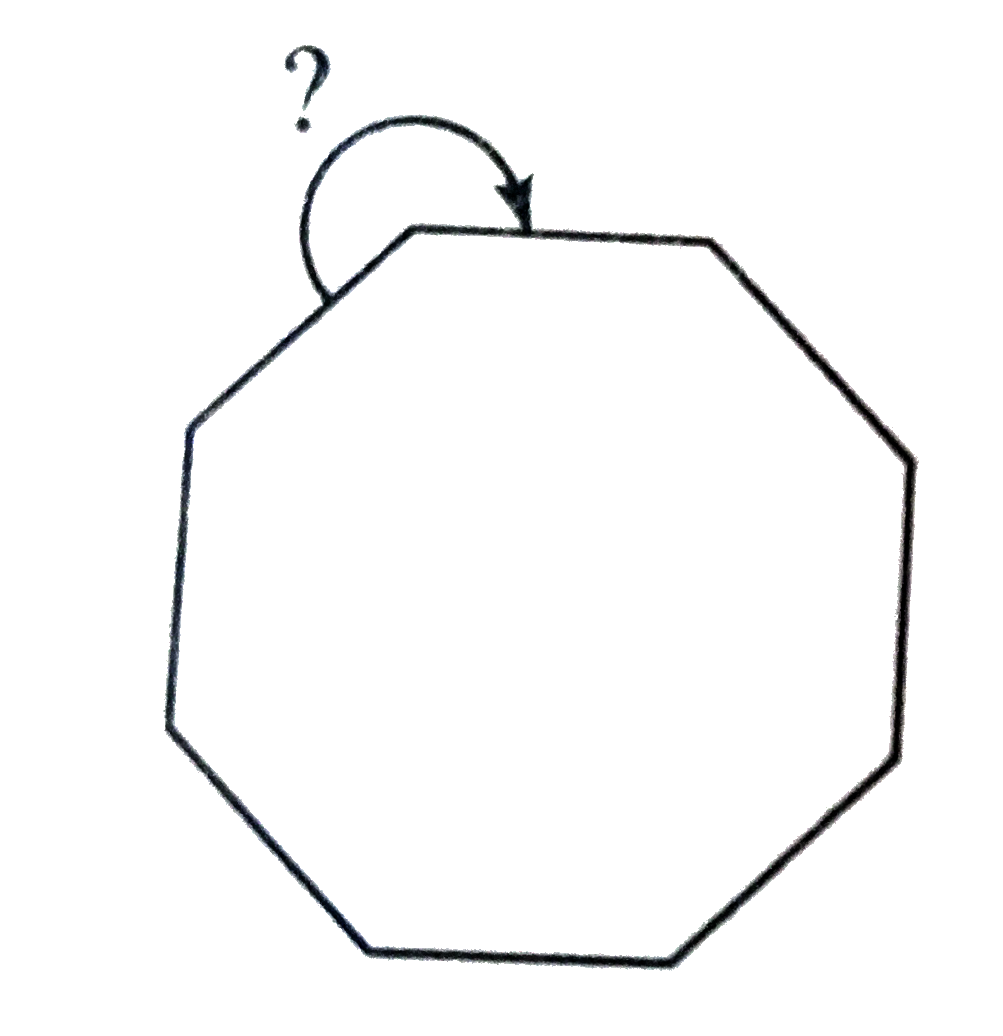
View SolutionThe measure of the sum of the interior angles of a regular n-sided polygon is (n-2)180∘. A regular octagon is shown below. What is the measure of the designated angle ?
View SolutionThe limit of the interior angle of a regular polygon of n sides as n→∞ is
View SolutionThe interior angle of a n sided regular polygon is 48∘ more than the interior angle of a regular hexagon. Find n.
View SolutionIn an n-sided regular polygon, each exterior angle is 72∘. Find the sum of all the interior angles of the polygon.
View SolutionThe interior angle of a n sided regular polygon is 48∘ more than the interior angle of a regular hexagon. Find n.
View SolutionThe sum of the internal angles of a regular polygon is 1440∘. The number of sides is :
View SolutionIf the sum of Interior angles of a regular polygon is equal to two times the sum of exterior angles of that polygon, then the number of sides of that polygon is
View SolutionFind the sum of the interior angles of a polygon of 8 sides.
View Solution8 भुजाओं वाले एक नियमित बहुभुज के सभी आंतरिक कोणों की माप का योग क्या होगा ?
View SolutionIf each interior angle of regular polygon is 144^(@) then what is the number of sides in the polygon
View SolutionConsider the following statements :
1. If n≥3 and m≥3 are distinct positive integers, then the sum of the exterior angles of a regular polygon of m sides is different from the sum of the exterior angles of a regular polygon of n sides.
2. Let m, n be integers such that m>n≥3. Then the sum of the interior angles of a regular polygon of m sides is greater than the sum of the interior angles of a regular polygon of n sides, and their sum is (m+n)π2.
Which of the above statements is/are correct?
View Solution
