In 2005, for each of the 14 million people present in a country, 0.028 were born and 0.008 died during the year. Using exponential equation, the number of people present in 2015 is predicted as
25 millions
17 millions
20 millions
18 millions
The correct Answer is:b
To solve the problem of predicting the population in 2015 based on the given birth and death rates, we can follow these steps:
Step 1: Identify the initial population and rates
- The initial population (N) in 2005 is 14 million.
- The birth rate (b) is 0.028.
- The death rate (d) is 0.008.
Step 2: Calculate the net growth rate (r)
- The net growth rate (r) is calculated by subtracting the death rate from the birth rate:
r=b−d=0.028−0.008=0.020
Step 3: Use the exponential growth formula
- The formula for exponential growth is given by:
N(t)=N0⋅ert
where:
- N(t) is the population at time t,
- N0 is the initial population,
- r is the net growth rate,
- t is the time in years,
- e is the base of the natural logarithm (approximately equal to 2.71828).
Step 4: Calculate the time period
- The time period from 2005 to 2015 is 10 years (t = 10).
Step 5: Substitute the values into the formula
- Substituting the values into the formula:
N(10)=14⋅e0.020⋅10
N(10)=14⋅e0.20
Step 6: Calculate e0.20
- Using a calculator, we find that e0.20 is approximately 1.2214.
Step 7: Calculate the predicted population
- Now, substituting this value back into the equation:
N(10)=14⋅1.2214≈17.1 million
Step 8: Round to the nearest million
- Rounding 17.1 million gives us approximately 17 million.
Conclusion
- Therefore, the predicted population in 2015 is approximately 17 million.
- The initial population (N) in 2005 is 14 million.
- The birth rate (b) is 0.028.
- The death rate (d) is 0.008.
- The net growth rate (r) is calculated by subtracting the death rate from the birth rate:
r=b−d=0.028−0.008=0.020
- The formula for exponential growth is given by:
N(t)=N0⋅ert
where:
- N(t) is the population at time t,
- N0 is the initial population,
- r is the net growth rate,
- t is the time in years,
- e is the base of the natural logarithm (approximately equal to 2.71828).
- The time period from 2005 to 2015 is 10 years (t = 10).
- Substituting the values into the formula:
N(10)=14⋅e0.020⋅10
N(10)=14⋅e0.20
- Using a calculator, we find that e0.20 is approximately 1.2214.
- Now, substituting this value back into the equation:
N(10)=14⋅1.2214≈17.1 million
- Rounding 17.1 million gives us approximately 17 million.
- Therefore, the predicted population in 2015 is approximately 17 million.
Topper's Solved these Questions
- BOOK - TRUEMEN BIOLOGY ENGLISHCHAPTER - NCERT Exemplar Questions +2 (MOLECULAR BASIS OF INHERITANCE)EXERCISE - MCQs28videos
NCERT Exemplar Questions +2 (MOLECULAR BASIS OF INHERITANCE)
- BOOK - TRUEMEN BIOLOGY ENGLISHCHAPTER - NCERT Exemplar Questions +2 (PRINCIPLE OF INHERITANCE AND VARIATION)EXERCISE - MCQs18videos
NCERT Exemplar Questions +2 (PRINCIPLE OF INHERITANCE AND VARIATION)
Similar Questions
The population of a certain is known to increase at a rate proportional to the number of people presently living in the country. If after two years the population has doubled, and after three years the population is 20,000 estimates the number of people initially living in the country.
View SolutionDr. John is a botanist , he is experimenting with exotic species of rose plant Rose polyantha . He started with 40 plants, after a year 22 more plants were added thought reproduction but also 14 plants died during the experimentation .
Which of the following statements are correct ?
1. The death rate is 0.35% per year
2. The birth rate is 0.55 % per rose per year
3. The birth rate is 0.55 % per year
4. The death rate is 0.35 % per rose per yearView Solution
Knowledge Check
- Question 1 - Select One
A marketing team conducted a study on the use of smartphones. In a certain metropolitan area, there were 1.6 million smartphone users at the end of 2018. The marketing team predicted that the number of smartphone users would increase by 35 percent each year beginning in 2019. If y represents the number of smartphone users in this metropolitan area after x years, then which of the following equations best models the number of smartphone users in this area over time ?
Ay=1,600,000(1.35)xBy=1,600,000(35)xCy=35+1,600,000Dy=1.35x+1,600,000 - Question 2 - Select One
Adriana used the data from a scatterplot she found on the U.S. Census Bureau's website to determine a regression model showing the relationship between the population in the area where she lived and the number of years, x, after she was born. The result was an exponential growth equation of the form y=x0(1+r)x. Which of the following does x0 most likely represent in the equation ?
AThe population in the year that she was bornBThe rate of change of the population over timeCThe maximum population reached during her lifetimeDThe number of years after her birth when the population reached its maximum - Question 3 - Select One
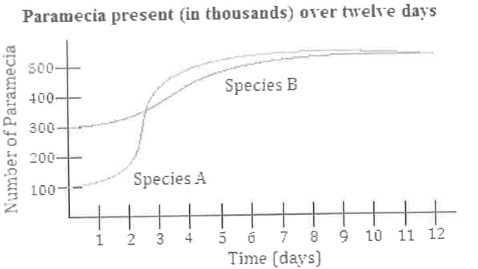
A small puddle is monitored by scientists for the number of paramecia present. The scientists are in two distinct species, let's call them ''species A'' and ''species B''. At time t = 0, the scientists measure and estimate the amount of species A and species B present in the puddle. They then proceed to measure and record the number of each species of paramecium present every hour for 12 days. the data for each species were then fit by a smooth curve, as shown in the graph above. Which of the following is a correct statement about the data above?AAt time t = 0, the number species B present is 150% greater than the number of species A presentBAt time t = 0, the number of species A present is 75% less than the number of species B presentCFor the first 3 days, the average growth rate of species B is higher than the average growth rate of species A.DThe growth rate of both rate of both species A and species B decreases for the last 8 days.
The 'wisdom of crowds" has become a mantra of the Internet age. Need to choose a new vacuum cleaner? Check out the reviews on online merchant Line Amazon. But a new study suggests that such online s scores don't always reveal the best choice. A massive controlled experiment of Web users finds that such ratings are highly susceptible to irrational "herd behavior' —and that the herd can be manipulated. Sometimes the crowd really is wiser than you. The to classic examples are guessing the weight of a bull or the number of gumballs in a jar. Your guess is probably going to be far from the mark, whereas the average of many people's choices is remarkably close to the true number. 15 But what happens when the goal is to judge something less tangible, such as the quality or worth of a product? According to one the, the wisdom of the crowd still holds—measuring ihe aggregate of people's opinions produces a stable, reliable 20 value, Skeptics, however, argue that people's opinions are easily swayed by those of others. So nudging a crowd early on by presenting contrary opinions—for example, exposing them to some very good or very bad attitudes—will steer the crowd in a 15 different direction. To test which hypothesis is true, you would need to manipulate huge numbers of people, exposing them to false information and determining how it affects their opinions. A team led b-y Sinan Aral, a network scientist at 30 the Massachusetts institute .of Technology in Cambridge, did exactly t lee Aral has been secretly . working with a popular website that aggregates news stories. The website allows users to make comments about news stories and vote each other's comments 55 up or down. The vote tallies ale visible as a number next to each comment , and the position of the comments is chronological. (Stories on the site get an average of about ten comments and about three votes per comment.)It’s a follow-up to his experiment using people’sratings of movies to measure how much individual people influence each other online (answer:alot).This time,he wanted to know how much the crowd influences the individual,and whether it can be controlled from outside.
For five months,every comment submitted by a user randomly received an“up”vote(positive),a “down”vote(negative),or as a control,no vote at all The team then observes! how users rated those comments. The users generated more than so 100,000 comments that were viewed more than 10 million times and rated more than 300,000 times by other users.
At least when it comes to comments on news sites, the crowd is more herdlike than wise. 55 Comments that received fake positive votes from the researchers were 32% more Likely to receive more positive votes compared with a control, the team reports. And those comments were no more likely than the control to be down-voted by the next viewer 60 to see them. By the end of the study, positively manipulated comments got an overall boost of about 25%. However, the same did not hold true for negative manipulation. The ratings of comments that got a fake down vote were usually negated by an up vote by the next user to see them. "Our experiment does not reveal the psychology behind people's decisions," Aral says, "but an intuitive explanation is that people are more skeptical of negative social influence. They're more 70 willing to go along with positive opinions from other people." - • -Duncan Watts, a network scientist at Microsoft Research in New York City, agrees with that conclusion. But] one question is whether the 75 positive 'herding] bias is specific to this site" or true in general, Watts says. lie points out that the category of the news items in the experiment had a strong effect on how much people could be manipulated. "I would have thought that 'business' is so pretty similar to 'economics,' yet they find a much stronger effect (almost 50% stronger) for the former • than the latter. What explains this difference? If we're going to apply these findings in the real world, we'll need to know the answers.Will companies be able to boost their products by manipulating online ratings on a massive scale? “That is easier said than done,”Wattssays.If people detect—or learn—that comments on a website are being manipulated,the herd may spook and leave entirely.
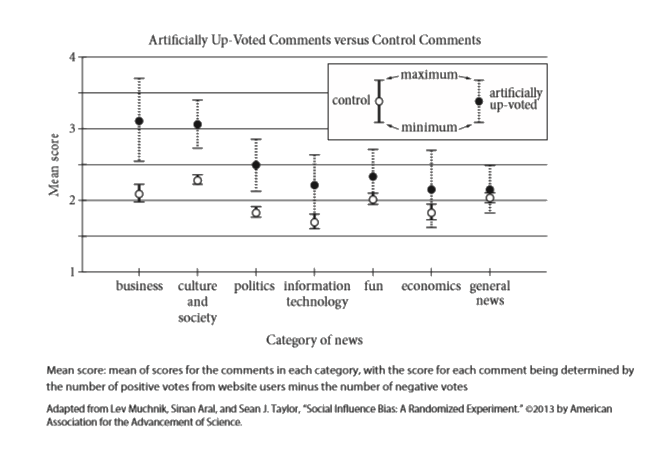
Over the course of the passage, the main focus shifts from a discussion of an experiment and its results toView SolutionThe 'wisdom of crowds" has become a mantra of the Internet age. Need to choose a new vacuum cleaner? Check out the reviews on online merchant Line Amazon. But a new study suggests that such online s scores don't always reveal the best choice. A massive controlled experiment of Web users finds that such ratings are highly susceptible to irrational "herd behavior' —and that the herd can be manipulated. Sometimes the crowd really is wiser than you. The to classic examples are guessing the weight of a bull or the number of gumballs in a jar. Your guess is probably going to be far from the mark, whereas the average of many people's choices is remarkably close to the true number. 15 But what happens when the goal is to judge something less tangible, such as the quality or worth of a product? According to one the, the wisdom of the crowd still holds—measuring ihe aggregate of people's opinions produces a stable, reliable 20 value, Skeptics, however, argue that people's opinions are easily swayed by those of others. So nudging a crowd early on by presenting contrary opinions—for example, exposing them to some very good or very bad attitudes—will steer the crowd in a 15 different direction. To test which hypothesis is true, you would need to manipulate huge numbers of people, exposing them to false information and determining how it affects their opinions. A team led b-y Sinan Aral, a network scientist at 30 the Massachusetts institute .of Technology in Cambridge, did exactly t lee Aral has been secretly . working with a popular website that aggregates news stories. The website allows users to make comments about news stories and vote each other's comments 55 up or down. The vote tallies ale visible as a number next to each comment , and the position of the comments is chronological. (Stories on the site get an average of about ten comments and about three votes per comment.)It’s a follow-up to his experiment using people’sratings of movies to measure how much individual people influence each other online (answer:alot).This time,he wanted to know how much the crowd influences the individual,and whether it can be controlled from outside.
For five months,every comment submitted by a user randomly received an“up”vote(positive),a “down”vote(negative),or as a control,no vote at all The team then observes! how users rated those comments. The users generated more than so 100,000 comments that were viewed more than 10 million times and rated more than 300,000 times by other users.
At least when it comes to comments on news sites, the crowd is more herdlike than wise. 55 Comments that received fake positive votes from the researchers were 32% more Likely to receive more positive votes compared with a control, the team reports. And those comments were no more likely than the control to be down-voted by the next viewer 60 to see them. By the end of the study, positively manipulated comments got an overall boost of about 25%. However, the same did not hold true for negative manipulation. The ratings of comments that got a fake down vote were usually negated by an up vote by the next user to see them. "Our experiment does not reveal the psychology behind people's decisions," Aral says, "but an intuitive explanation is that people are more skeptical of negative social influence. They're more 70 willing to go along with positive opinions from other people." - • -Duncan Watts, a network scientist at Microsoft Research in New York City, agrees with that conclusion. But] one question is whether the 75 positive 'herding] bias is specific to this site" or true in general, Watts says. lie points out that the category of the news items in the experiment had a strong effect on how much people could be manipulated. "I would have thought that 'business' is so pretty similar to 'economics,' yet they find a much stronger effect (almost 50% stronger) for the former • than the latter. What explains this difference? If we're going to apply these findings in the real world, we'll need to know the answers.Will companies be able to boost their products by manipulating online ratings on a massive scale? “That is easier said than done,”Wattssays.If people detect—or learn—that comments on a website are being manipulated,the herd may spook and leave entirely.
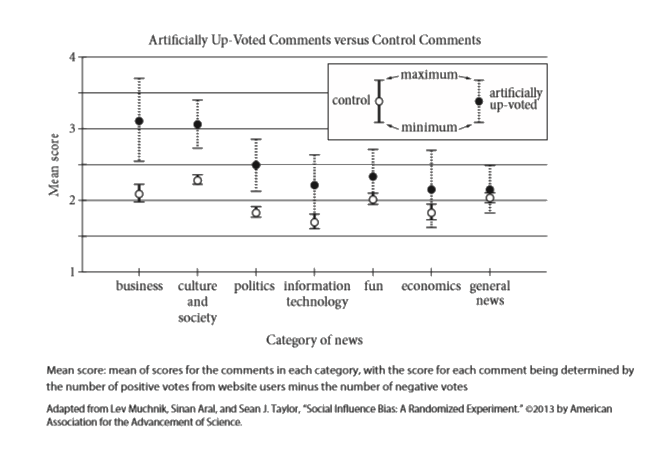
As used in line 85,"boost"most nearly meansView SolutionThe 'wisdom of crowds" has become a mantra of the Internet age. Need to choose a new vacuum cleaner? Check out the reviews on online merchant Line Amazon. But a new study suggests that such online s scores don't always reveal the best choice. A massive controlled experiment of Web users finds that such ratings are highly susceptible to irrational "herd behavior' —and that the herd can be manipulated. Sometimes the crowd really is wiser than you. The to classic examples are guessing the weight of a bull or the number of gumballs in a jar. Your guess is probably going to be far from the mark, whereas the average of many people's choices is remarkably close to the true number. 15 But what happens when the goal is to judge something less tangible, such as the quality or worth of a product? According to one the, the wisdom of the crowd still holds—measuring ihe aggregate of people's opinions produces a stable, reliable 20 value, Skeptics, however, argue that people's opinions are easily swayed by those of others. So nudging a crowd early on by presenting contrary opinions—for example, exposing them to some very good or very bad attitudes—will steer the crowd in a 15 different direction. To test which hypothesis is true, you would need to manipulate huge numbers of people, exposing them to false information and determining how it affects their opinions. A team led b-y Sinan Aral, a network scientist at 30 the Massachusetts institute .of Technology in Cambridge, did exactly t lee Aral has been secretly . working with a popular website that aggregates news stories. The website allows users to make comments about news stories and vote each other's comments 55 up or down. The vote tallies ale visible as a number next to each comment , and the position of the comments is chronological. (Stories on the site get an average of about ten comments and about three votes per comment.)It’s a follow-up to his experiment using people’sratings of movies to measure how much individual people influence each other online (answer:alot).This time,he wanted to know how much the crowd influences the individual,and whether it can be controlled from outside.
For five months,every comment submitted by a user randomly received an“up”vote(positive),a “down”vote(negative),or as a control,no vote at all The team then observes! how users rated those comments. The users generated more than so 100,000 comments that were viewed more than 10 million times and rated more than 300,000 times by other users.
At least when it comes to comments on news sites, the crowd is more herdlike than wise. 55 Comments that received fake positive votes from the researchers were 32% more Likely to receive more positive votes compared with a control, the team reports. And those comments were no more likely than the control to be down-voted by the next viewer 60 to see them. By the end of the study, positively manipulated comments got an overall boost of about 25%. However, the same did not hold true for negative manipulation. The ratings of comments that got a fake down vote were usually negated by an up vote by the next user to see them. "Our experiment does not reveal the psychology behind people's decisions," Aral says, "but an intuitive explanation is that people are more skeptical of negative social influence. They're more 70 willing to go along with positive opinions from other people." - • -Duncan Watts, a network scientist at Microsoft Research in New York City, agrees with that conclusion. But] one question is whether the 75 positive 'herding] bias is specific to this site" or true in general, Watts says. lie points out that the category of the news items in the experiment had a strong effect on how much people could be manipulated. "I would have thought that 'business' is so pretty similar to 'economics,' yet they find a much stronger effect (almost 50% stronger) for the former • than the latter. What explains this difference? If we're going to apply these findings in the real world, we'll need to know the answers.Will companies be able to boost their products by manipulating online ratings on a massive scale? “That is easier said than done,”Wattssays.If people detect—or learn—that comments on a website are being manipulated,the herd may spook and leave entirely.
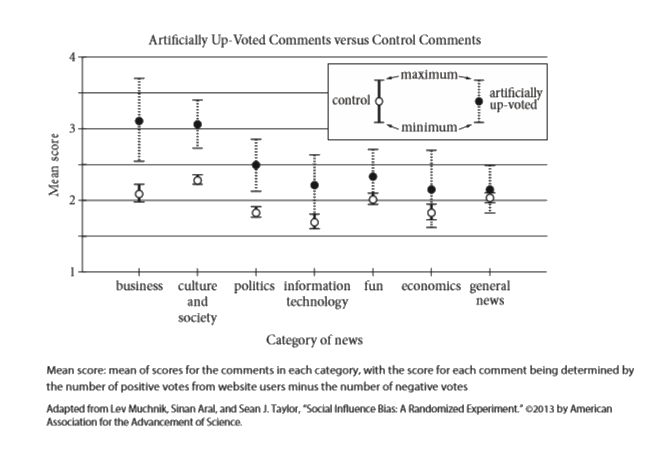
Which action would best address a question watts raises about the study?View SolutionThe 'wisdom of crowds" has become a mantra of the Internet age. Need to choose a new vacuum cleaner? Check out the reviews on online merchant Line Amazon. But a new study suggests that such online s scores don't always reveal the best choice. A massive controlled experiment of Web users finds that such ratings are highly susceptible to irrational "herd behavior' —and that the herd can be manipulated. Sometimes the crowd really is wiser than you. The to classic examples are guessing the weight of a bull or the number of gumballs in a jar. Your guess is probably going to be far from the mark, whereas the average of many people's choices is remarkably close to the true number. 15 But what happens when the goal is to judge something less tangible, such as the quality or worth of a product? According to one the, the wisdom of the crowd still holds—measuring ihe aggregate of people's opinions produces a stable, reliable 20 value, Skeptics, however, argue that people's opinions are easily swayed by those of others. So nudging a crowd early on by presenting contrary opinions—for example, exposing them to some very good or very bad attitudes—will steer the crowd in a 15 different direction. To test which hypothesis is true, you would need to manipulate huge numbers of people, exposing them to false information and determining how it affects their opinions. A team led b-y Sinan Aral, a network scientist at 30 the Massachusetts institute .of Technology in Cambridge, did exactly t lee Aral has been secretly . working with a popular website that aggregates news stories. The website allows users to make comments about news stories and vote each other's comments 55 up or down. The vote tallies ale visible as a number next to each comment , and the position of the comments is chronological. (Stories on the site get an average of about ten comments and about three votes per comment.)It’s a follow-up to his experiment using people’sratings of movies to measure how much individual people influence each other online (answer:alot).This time,he wanted to know how much the crowd influences the individual,and whether it can be controlled from outside.
For five months,every comment submitted by a user randomly received an“up”vote(positive),a “down”vote(negative),or as a control,no vote at all The team then observes! how users rated those comments. The users generated more than so 100,000 comments that were viewed more than 10 million times and rated more than 300,000 times by other users.
At least when it comes to comments on news sites, the crowd is more herdlike than wise. 55 Comments that received fake positive votes from the researchers were 32% more Likely to receive more positive votes compared with a control, the team reports. And those comments were no more likely than the control to be down-voted by the next viewer 60 to see them. By the end of the study, positively manipulated comments got an overall boost of about 25%. However, the same did not hold true for negative manipulation. The ratings of comments that got a fake down vote were usually negated by an up vote by the next user to see them. "Our experiment does not reveal the psychology behind people's decisions," Aral says, "but an intuitive explanation is that people are more skeptical of negative social influence. They're more 70 willing to go along with positive opinions from other people." - • -Duncan Watts, a network scientist at Microsoft Research in New York City, agrees with that conclusion. But] one question is whether the 75 positive 'herding] bias is specific to this site" or true in general, Watts says. lie points out that the category of the news items in the experiment had a strong effect on how much people could be manipulated. "I would have thought that 'business' is so pretty similar to 'economics,' yet they find a much stronger effect (almost 50% stronger) for the former • than the latter. What explains this difference? If we're going to apply these findings in the real world, we'll need to know the answers.Will companies be able to boost their products by manipulating online ratings on a massive scale? “That is easier said than done,”Wattssays.If people detect—or learn—that comments on a website are being manipulated,the herd may spook and leave entirely.

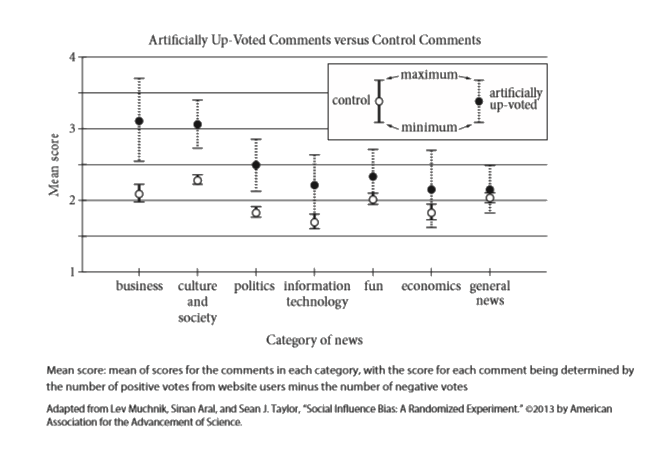
In the figure, which category of news have an artifically up-voted mean square of 2.5?View SolutionThe 'wisdom of crowds" has become a mantra of the Internet age. Need to choose a new vacuum cleaner? Check out the reviews on online merchant Line Amazon. But a new study suggests that such online s scores don't always reveal the best choice. A massive controlled experiment of Web users finds that such ratings are highly susceptible to irrational "herd behavior' —and that the herd can be manipulated. Sometimes the crowd really is wiser than you. The to classic examples are guessing the weight of a bull or the number of gumballs in a jar. Your guess is probably going to be far from the mark, whereas the average of many people's choices is remarkably close to the true number. 15 But what happens when the goal is to judge something less tangible, such as the quality or worth of a product? According to one the, the wisdom of the crowd still holds—measuring ihe aggregate of people's opinions produces a stable, reliable 20 value, Skeptics, however, argue that people's opinions are easily swayed by those of others. So nudging a crowd early on by presenting contrary opinions—for example, exposing them to some very good or very bad attitudes—will steer the crowd in a 15 different direction. To test which hypothesis is true, you would need to manipulate huge numbers of people, exposing them to false information and determining how it affects their opinions. A team led b-y Sinan Aral, a network scientist at 30 the Massachusetts institute .of Technology in Cambridge, did exactly t lee Aral has been secretly . working with a popular website that aggregates news stories. The website allows users to make comments about news stories and vote each other's comments 55 up or down. The vote tallies ale visible as a number next to each comment , and the position of the comments is chronological. (Stories on the site get an average of about ten comments and about three votes per comment.)It’s a follow-up to his experiment using people’sratings of movies to measure how much individual people influence each other online (answer:alot).This time,he wanted to know how much the crowd influences the individual,and whether it can be controlled from outside.
For five months,every comment submitted by a user randomly received an“up”vote(positive),a “down”vote(negative),or as a control,no vote at all The team then observes! how users rated those comments. The users generated more than so 100,000 comments that were viewed more than 10 million times and rated more than 300,000 times by other users.
At least when it comes to comments on news sites, the crowd is more herdlike than wise. 55 Comments that received fake positive votes from the researchers were 32% more Likely to receive more positive votes compared with a control, the team reports. And those comments were no more likely than the control to be down-voted by the next viewer 60 to see them. By the end of the study, positively manipulated comments got an overall boost of about 25%. However, the same did not hold true for negative manipulation. The ratings of comments that got a fake down vote were usually negated by an up vote by the next user to see them. "Our experiment does not reveal the psychology behind people's decisions," Aral says, "but an intuitive explanation is that people are more skeptical of negative social influence. They're more 70 willing to go along with positive opinions from other people." - • -Duncan Watts, a network scientist at Microsoft Research in New York City, agrees with that conclusion. But] one question is whether the 75 positive 'herding] bias is specific to this site" or true in general, Watts says. lie points out that the category of the news items in the experiment had a strong effect on how much people could be manipulated. "I would have thought that 'business' is so pretty similar to 'economics,' yet they find a much stronger effect (almost 50% stronger) for the former • than the latter. What explains this difference? If we're going to apply these findings in the real world, we'll need to know the answers.Will companies be able to boost their products by manipulating online ratings on a massive scale? “That is easier said than done,”Wattssays.If people detect—or learn—that comments on a website are being manipulated,the herd may spook and leave entirely.
As used in line 86,"Scale" most nearly meansView Solution

