The rate constant for the first order decomposition of H2O2 is given by the following equation :
logk=14.34−1.25×104K/T
Calculate Ea for this reaction and at what temperature will its half-period be 256 minutes?
According to Arrhenius equation
k=Ae−Ea/RT
Taking logarithm of both sides,
In k=In A−EaRTorlogk=logA−Ea2.303RT
Equating similar terms in the two equations
Ea2.303RT=1.25×104KTorEa=2.303R×1.25×104K
or Ea=2.303×(8.314JK−1mol−1)×1.25×104K=239.34kJ mol−1
When t1/2=256min,k=0.693256×60s=4.51×10−5s−1
Substituting this value in the given equation, we get
log(4.51×10−5)=14.34−1.25×104KT
or (−5+0.6542)=14.34−1.25×104KT
or 1.25×104KT=18.6858orT=669K.
Topper's Solved these Questions
- CHEMICAL KINETICS BOOK - U-LIKE SERIESCHAPTER - CHEMICAL KINETICS EXERCISE - CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS
15 Videos
- CHEMICAL KINETICS BOOK - U-LIKE SERIESCHAPTER - CHEMICAL KINETICS EXERCISE - MULTIPLE CHOICE QUESTIONS
19 Videos
- CHEMICAL KINETICS BOOK - U-LIKE SERIESCHAPTER - CHEMICAL KINETICS EXERCISE - SELF ASSESSMENT TEST (SECTION D)
1 Videos
- CBSE EXAMINATION PAPER 2020 (CODE No.56/4/1) BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (CODE No.56/4/1) EXERCISE - SECTION -D
3 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - U-LIKE SERIESCHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - LONG ANSWER QUESTIONS - I
21 Videos
Similar Questions
The rate constant for the first order decompoistion of a certain reaction is described by the equation
logk(s−1)=14.34−1.25×104KT
(a) What is the energy of activation for the reaction?
(b) At what temperature will its half-life periof be 256min?
View SolutionThe rate constant for the first order decomposition of H2O2 is given by the following equation :
logk=14.2−1.0×104T
Calculate Ea for this reaction and rate constant k if its half-life period be 200 minutes.
[Given : R=8.314JK−1mol−1]
View Solution
Knowledge Check
The rate constant for the first order decomposition of ethylene oxide into CH4 and CO,
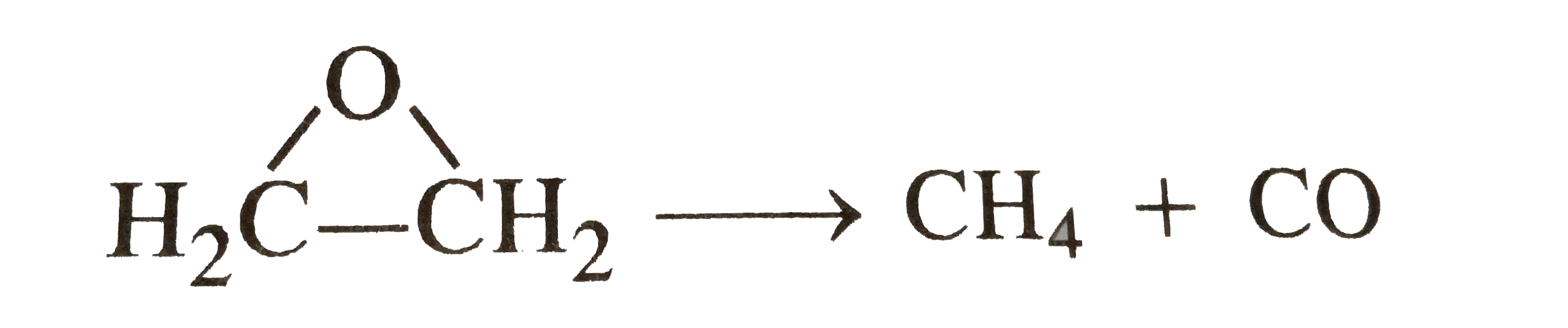
may be describe by
logk(ins−1)=14.34−1.25×104KT
The activation energy of the reaction isA4.8×10−5kJmol−1B4.8×105kJmol−1C2.39×102kJmol−1D2.39×105kJmol−1
The rate constant for the first order decomposition of H2O2 is given by the following equation : log K = 14.2 - 1.0×104TK
Calculate Ea for this reaction and rate constant k if its half life period be 200 minutes. (Given : R = 8.314 JK−1mol−1)
View SolutionThe rate constant for the first order decomposition of H2O2 is given by the following equation : log K = 14.2 - 1.0×104TK
Calculate E for this reaction and rate constant k if its half life period be 200 minutes. (Given : R = 8.314 JK−1mol−1)
View SolutionThe rate constant for the first order decomposition of N2O5 is given by the following equation: k=(2.5×1014s−1)e(−25000K)/T
Calculate Ea for this reaction and rate constant if its half-life period be 300 minutes.
View SolutionThe rate constant for the first order decompoistion of a certain reaction is described by the equation
logk(s−1)=14.34−1.25×104KT
(a) What is the energy of activation for the reaction?
(b) At what temperature will its half-life periof be 256min?
View SolutionThe rate constant for the first order decomposition of a certain reaction is described by the equation
logk(s−1)=14.34−1.25×104KT
(a) What is the energy of activation for the reaction?
(b) At what temperature will its half-life period be 256min?
View SolutionThe rate constant for the first order decompoistion of a certain reaction is described by the equation
logk(s−1)=14.34−1.25×104KT
(a) What is the energy of activation for the reaction?
(b) At what temperature will its half-life periof be 256min?
View SolutionThe rate constant of a first order reaction of H2O2 is given by log k=14.341.25*10^4k/t. Calculate Ea for this reaction and at what temperature, the half-life of the reaction is 256 min?
View Solution
